ИДЗ-2. Действия с матрицами

Даны две матрицы A и B:

A = 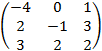; B = .

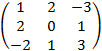Найти: а) AB; б) BA; в) A^–1; г) AA^–1; д) A^–1A.

Решение: а) AB = × =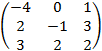

= = .

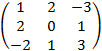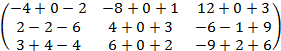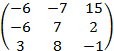б) BA = × =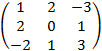

= = .

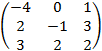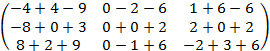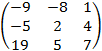Можно заметить, что AB ¹ BA, т.е. в общем случае операция умножения матриц неперестановочна.

в) Вычислим обратную матрицу A^–1. Как известно, обратная матрица к данной матрице A может быть найдена по формуле:

A^–1 = × ,

где D = 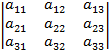– определитель матрицы A; A* = – транспонированная матрица алгебраических дополнений к элементам a_ij исходной матрицы A (присоединенная матрица). Обратная матрица A^–1 существует при D ¹ 0.

Определитель данной матрицы A равен:

D = 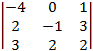= = 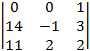1× 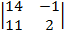= 14×2 – 11×(–1) = 39 ¹ 0.

Вычислим алгебраические дополнения к элементам матрицы A:

A₁₁ = (–1)¹⁺¹× = (–1)×2 – 2×3 = –8;

A₁₂ = (–1)¹⁺²× = –(2×2 – 3×3) = 5;

A₁₃ = (–1)¹⁺³× 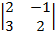= 2×2 – 3×(–1) = 7;

A₂₁ = (–1)²⁺¹× = –(0×2 – 1×2) = 2;

A₂₂ = (–1)²⁺²× = (–4)×2 – 3×1 = –11;

A₂₃ = (–1)²⁺³× = –((–4)×2 – 3×0) = 8;

A₃₁ = (–1)³⁺¹× 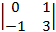= 0×3 – (–1)×1 = 1;

A₃₂ = (–1)³⁺²× 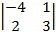= –((–4)×3 – 2×1) = 14;

A₃₃ = (–1)³⁺³× = (–4)×(–1) – 2×0 = 4;

Таким образом, матрица алгебраических дополнений матрицы A есть 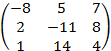; транспонированная к ней матрица (присоединенная матрица) A* = 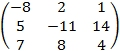. Наконец, обратная матрица матрицы A равна:

A^–1 = × .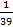

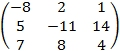г) Удостоверимся в правильности расчетов, вычислив произведение AA^–1:

AA^–1 = × × = × × =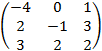

= × = × = .

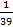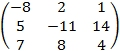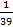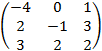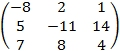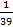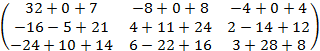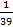д) Удостоверимся в правильности расчетов, вычислив произведение A^–1A:

A^–1A = × × =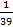

= × = × = .

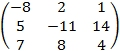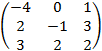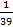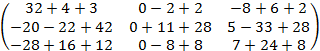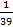Как видно, AA^–1 = A^–1A = E, где E – единичная матрица. Это значит, что матрица A^–1 вычислена правильно.

Ответ: а) AB = 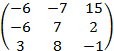; б) BA = ;

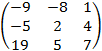в) A^–1 = 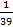× 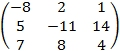; г), д) AA^–1 = A^–1A = E.