ФУНКЦИИ

Определение 1.2.1. Пусть X и Y – некоторые числовые множества и пусть каждому элементу 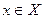по какому-либо закону f поставлен только один элемент 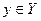. Тогда говорят, что на множестве Х задана функция .

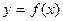При этом переменную x называют независимой переменной (или аргументом), y – зависимой переменной, множество Х – областью определения функции, множество Y – областью значений функции.

Три способа задания функции:

1. Табличный. Этот способ имеет широкое применение в различных отраслях: экспериментальных измерениях, таблицах бухгалтерской отчетности и банковской деятельности, статистических данных и т.п. Как правило, в таких таблицах одну из переменных можно принять за независимую, тогда другие величины будут являться функциями от этого аргумента.

2. Аналитический. Этот способ состоит в задании связи между аргументом и функцией в виде формулы или набора формул.

Примеры:

1) .

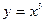2) .

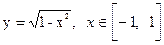3)

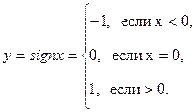
(Название sign происходит от латинского signum – знак).

3. Графический. Соответствие между аргументом и функцией задается посредством графика. В экономике широко применяются графики, характеризующие динамику экономических параметров: объема ВВП, выручки, курса валют и т.п.

Основные свойства функции.

1. Четность (нечетность). Функция 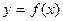называется четной (симметрия относительно оси ординат), если для любых значений аргумента из области определения выполняется условие .

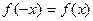Функция 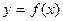называется нечетной (симметрия относительно начала координат), если для любых 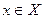выполнено условие .

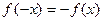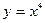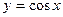Например, функции и являются четными, а функци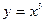и и 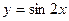- нечетными.

2. Монотонность. Функция 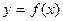называется возрастающей (убывающей) на некотором промежутке Х, если большему значению аргумента соответствует большее (меньшее) значение функции f(x).

3. Ограниченность. Функция 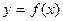называется ограниченной на промежутке Х, если существует такое число М>0, что для всех . В противном случае функция называется неограниченной.

4. Периодичность. Функция 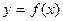называется периодической с периодом , если для любых .

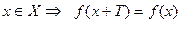Пример 1. Найти область определения функции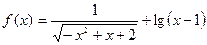

Решение. Так как данная функция представляет собой сумму функций, то область определения будет состоять из всех тех значений x, которые принадлежат одновременно области определения функци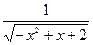й и 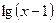. Поэтому, достаточно решить следующую систему неравенств:

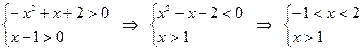
Таким образом, область определения функции есть интервал (1, 2).