ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ И ЕЕ ПРЕДЕЛЫ

Определение 1.1.1.Если каждому значению n из натурального ряда чисел 1, 2, …n ставится в соответствии по определенному закону некоторое вещественное число x_n, то множество занумерованных вещественных чисел будет называться числовой последовательностью íx_пý.

Примеры:

1) ín²ý=1, 2², 3²….,n²…

2) í1+(-1)ⁿý=0, 2, 0, 2,…

3) í 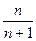ý=

Определение 1.1.2. Последовательность íx_пý называется ограниченной сверху (снизу), если существует вещественное число M (соответственно m), такое что для всех элементов x_n выполняется неравенство:

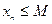(соответственно 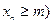(1.1.1)

При этом, число M (m) называется верхней гранью (нижней гранью), а неравенство 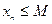( 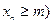условием ограниченности.

Определение 1.1.3. Последовательность íx_пý называется ограниченной, если она ограничена и сверху и снизу, то есть если существуют вещественные числа m и М, такие что для всех элементов x_n выполняется условие:

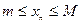(1.1.2)

Примеры:

1) Последовательность í 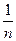ý= 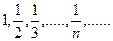является ограниченной, так как любой ее элемент 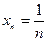удовлетворяет условию (2) при любых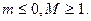

2) Последовательность ín²ý=1, 2², 3²….,n²… ограничена снизу m=1 и неограниченна сверху.

Рассмотрим последовательность чисел:

х₁, х₂, х₃,…., х_n……

Определение 1.1.4. Число a называется пределом последовательности íх_пý, если для любого e > 0 найдется такой номер N(e), что при n > N(e) выполняется неравенство

êх_n - a ú < e (1.1.3)

Последовательность, имеющая предел, называется сходящейся и записывается это следующим образом:

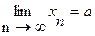
Пример 1. Доказать по определению предела последовательности чисел, что .

Возьмем любое число

Посмотрим, при каких номерах (п) будет выполняться неравенство

(*) ,

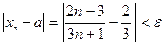где e - любое положительное число?