Понятие дифференциала.
Если функция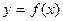 
дифференцируема в точке 
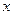, то есть имеет в этой точке конечную производную 
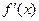, то ее приращение 
можно записать в виде
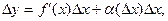
где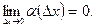 
Главная, линейная относительно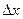 
часть 
приращения функции называется дифференциаломфункции и обозначается dy:
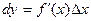
Положив в формуле дифференциала 
, получим 
. Тогда окончательно получим:
Дата добавления: 2014-12-04; просмотров: 841;