Абсолютне прискорення точки при складному русі дорівнює геометричній сумі відносного, переносного прискорень та прискорення Коріоліса.

Для доведення цієї теореми скористаємося рівністю (19.2) для абсолютної швидкості точки. Диференціюючи рівність (19.2) за часом і групуючи подібні доданки, одержимо такий вираз абсолютного прискорення точки:

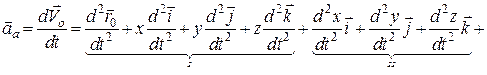
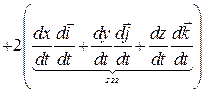. (19.7)

Проаналізуємо вираз (19.7), розбивши його на три групи доданків: І, ІІ, ІІІ.

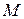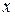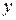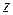Якщо зупинити рух точки відносно рухомої системи, тобто вважати координати , , – сталими, то доданки другої та третьої груп дорівнюватимуть нулеві.

Перша група доданків (І), що залишилася, є прискоренням тієї точки рухомої системи, з якою в даний момент збігається точка 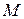, тобто це переносне прискорення .

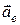Переносне прискорення точки в складному русі характеризує зміну її переносної швидкості в переносному русі і визначається за правилами визначення прискорення точки твердого тіла.

Якщо зупинити рухому систему координат, тобто вважати 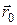, , 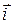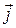і 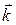– сталими, то доданки першої і третьої груп, які містять похідні від вказаних величин за часом, будуть дорівнювати нулю.

Друга група доданків (ІІ) є прискоренням точки 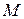відносно рухомої системи координат , тобто це відносне прискорення .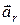

Відносне прискорення точки в складному русі характеризує зміну відносної швидкості у відносному русі і визначається за правилами кінематики точки, якщо вважати рухому систему зупиненою.

Третя група доданків (ІІІ) не може бути віднесена ні до відносного, ні до переносного прискорення, оскільки у цю групу входять 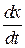, , 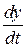, 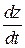які залежать від відносного руху точки, та 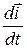, , 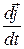, 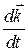що залежать від руху рухомої системи.

Прискорення, яке визначається групою ІІІ доданків, називається прискоренням Коріоліса і позначається .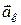

Рівність (19.7) з урахуванням позначень, відносно груп доданків ( 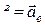, , 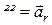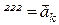) остаточно набуває вигляду:

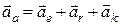. (19.8)

Таким чином , теорему доведено.

Вперше теорема (19.8) була сформульована Ейлером, доведена Гауссом, а узагальнив її французський вчений Коріоліс.