Визначення формули прискорення Коріоліса

Розглянемо тепер вираз прискорення Коріоліса, тобто третю групу доданків (ІІІ) в формулі (19.7) і надамо більш зручну форму запису цього прискорення.

Нехай переносний рух, тобто рух рухомої системи, є обертальним навколо нерухомої осі 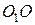з кутовою швидкістю 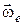. Вектор 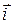можна розглядати як радіус-вектор точки 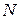відносно точки 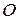(рис. 20.1). Тому швидкість цієї точки дорівнює:

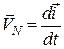. (20.1)

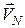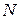Але при обертальному русі рухомої системи швидкість точки визначається і за формулою Ейлера ( 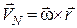), для якої радіусом-вектором є орт 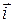, тоді

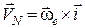. (20.2)

Порівнюючи (20.1) і (20.2), знаходимо, що 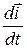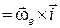. Аналогічно:

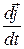
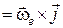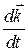
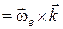, . (20.3)

Підставимо значення похідних за часом від ортів рухомої системи (20.3) у вираз прискорення Коріоліса, тобто у групу доданків ІІІ із виразу (19.7):

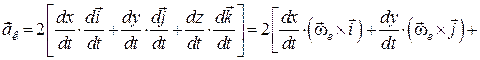
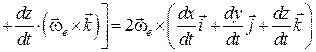. (20.4)

Як відомо з (20.3), вираз у дужках рівняння (20.12) – це вектор відносної швидкості точки .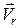

Отже, для вектора прискорення Коріоліса остаточно маємо:

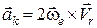. (20.5)