Визначення прискорень точок плоскої фігури за допомогою миттєвого центра прискорень
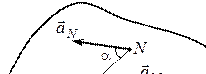 Нехай точка
Нехай точка 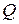 є миттєвим центром прискорень, тобто
є миттєвим центром прискорень, тобто 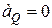 .
.
Якщо прийняти миттєвий центр прискорень за полюс, то прискорення будь-якої точки плоскої фігури визначається як прискорення цієї точки у обертальному русі навколо миттєвого центру прискорень (рис. 18.4):
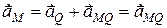 ;
;
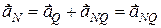 , (18.14)
, (18.14)
де 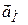 спрямований під кутом
спрямований під кутом 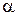 до відрізка
до відрізка 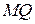 ,
, 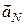 спрямований під кутом
спрямований під кутом 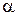 до відрізка
до відрізка 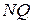 і т.д.
і т.д.
За модулем прискорення точок визначаються формулами:
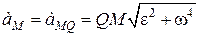 ,
,
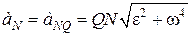 ,… (18.15)
,… (18.15)
Звідки випливає, що
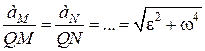 . (18.16)
. (18.16)
Отже, прискорення точок плоскої фігури в кожний момент часу пропорційні відстаням цих точок від миттєвого центра прискорень і направлені під одним і тим же кутом 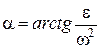 до відрізків, що з'єднують ці точки з миттєвим центром прискорень, у бік обертання, якщо
до відрізків, що з'єднують ці точки з миттєвим центром прискорень, у бік обертання, якщо 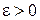 і в протилежний бік, якщо
і в протилежний бік, якщо 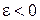 (рис. 18.4).
(рис. 18.4).
Таким чином, при обчисленні прискорень точок плоскої фігури можна вважати, що плоска фігура в даний момент обертається навколо миттєвого центра прискорень.
18.4. Випадки визначення положення миттєвого центра прискорень (МЦП)
 Випадок 1. Якщо відома точка тіла, прискорення якої у даний момент часу дорівнює нулю, тобто вона і буде МЦП (рис. 18.5). Колесо котиться без ковзання за прямолінійною рейкою зі сталою швидкістю центра
Випадок 1. Якщо відома точка тіла, прискорення якої у даний момент часу дорівнює нулю, тобто вона і буде МЦП (рис. 18.5). Колесо котиться без ковзання за прямолінійною рейкою зі сталою швидкістю центра 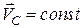 . Тоді
. Тоді 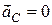 і точка
і точка 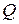 співпадає з центром колеса
співпадає з центром колеса 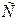 . Прискорення точок, які лежать на ободі колеса спрямовані уздовж відповідних радіусів до центру колеса і становлять:
. Прискорення точок, які лежать на ободі колеса спрямовані уздовж відповідних радіусів до центру колеса і становлять:
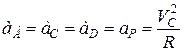 .
.
Прискорення точки 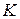 , яка лежить на відстані
, яка лежить на відстані 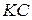 відцентру, становить
відцентру, становить 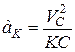 і спрямоване до центру колеса
і спрямоване до центру колеса 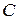 .
.
Зауважимо, що миттєвий центр прискорень 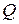 не збігається з миттєвим центром швидкостей
не збігається з миттєвим центром швидкостей 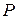 даної плоскої фігури. Це різні точки (рис. 18.5).
даної плоскої фігури. Це різні точки (рис. 18.5).
Випадок ІІ. У даний момент відомі модуль і напрям прискорення 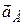 точки А, а також напрями і величини кутової швидкості і кутового прискорення, тобто
точки А, а також напрями і величини кутової швидкості і кутового прискорення, тобто 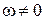 ;
; 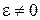 (рис. 18.6).
(рис. 18.6).
У цьому випадку МЦП лежить на відрізку, що утворює з напрямом вектора 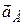 кут
кут 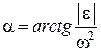 , який відраховується від
, який відраховується від 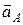 у бік напряму
у бік напряму 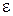 . Відстань від точки А до МЦП дорівнює:
. Відстань від точки А до МЦП дорівнює:
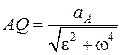 .
.
Випадок ІІІ. У даний момент часу відомі модулі і напрям прискорення 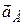 точки А, а також що
точки А, а також що 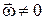 , а
, а 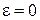 (рис. 18.7). У цьому випадку
(рис. 18.7). У цьому випадку 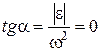 . Тобто
. Тобто 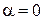 і МЦП розташований на промені вектора
і МЦП розташований на промені вектора 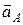 . Його відстань від точки
. Його відстань від точки 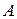 визначається за формулою:
визначається за формулою: 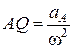 ;
;
У випадку, коли 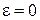 , а
, а 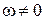 , миттєвий центр прискорень лежить у точці перетину прямих, за якими спрямовані прискорення точок плоскої фігури (рис. 18.8).
, миттєвий центр прискорень лежить у точці перетину прямих, за якими спрямовані прискорення точок плоскої фігури (рис. 18.8).
 |
Випадок ІV. У даний момент часу відому модуль і напрям прискорення
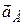 точки
точки 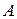 , а також що
, а також що 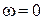 ,
, 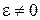 . У цьому випадку
. У цьому випадку 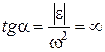 , тобто
, тобто 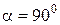 і МЦП, розташований на перпендикулярі до вектора
і МЦП, розташований на перпендикулярі до вектора 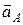 . Його відстань від точки
. Його відстань від точки 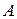 визначається за формулою
визначається за формулою 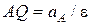 (рис. 18.9).
(рис. 18.9).
У випадку, коли 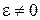 , а
, а 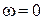 миттєвий центр прискорень лежить у точці перетину перпендикулярів до векторів прискорень точок плоскої фігури, проведених з цих точок (рис. 18.10).
миттєвий центр прискорень лежить у точці перетину перпендикулярів до векторів прискорень точок плоскої фігури, проведених з цих точок (рис. 18.10).
Випадок V. Якщо відомі прискорення 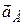 і
і 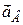 двох точок плоскої фігури, то миттєвий центр прискорень
двох точок плоскої фігури, то миттєвий центр прискорень 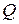 знаходиться у точці перетину променів, які виходять з цих точок під кутом
знаходиться у точці перетину променів, які виходять з цих точок під кутом 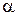 , що утворює вектор
, що утворює вектор 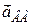 з відрізком
з відрізком 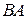 , і цей кут потрібно відкладати від векторів
, і цей кут потрібно відкладати від векторів 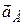 і
і 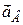 за напрямом
за напрямом 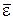 (рис. 18.11).
(рис. 18.11).
 |
Дійсно, щоб знайти миттєвий центр прискорень, приймаємо одну з цих точок, наприклад точку
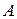 , за полюс. На підставі (18.8) одержимо
, за полюс. На підставі (18.8) одержимо
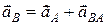 .
.
Звідки прискорення 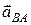 точки
точки 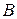 у обертальному русі навколо точки
у обертальному русі навколо точки 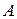 дорівнюватиме:
дорівнюватиме: 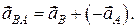
Побудувавши у точці 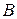 паралелограм на векторах
паралелограм на векторах 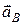 і (
і ( 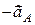 ), знайдемо
), знайдемо 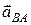 і кут
і кут 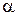 , який утворює вектор
, який утворює вектор 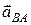 з відрізком
з відрізком 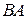 , а разом з тим і напрям
, а разом з тим і напрям 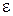 (рис. 18.11).
(рис. 18.11).
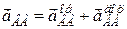 ;
;
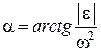 .
.
 |
Потім з точок
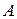 і
і 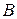 проведемо промені
проведемо промені 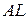 і
і 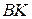 під кутом
під кутом 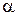 відповідно до
відповідно до 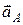 і
і 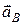 , відкладеним за напрямом
, відкладеним за напрямом 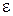 . У точці перетину цих прямих і буде знаходитись миттєвий центр прискорень точки
. У точці перетину цих прямих і буде знаходитись миттєвий центр прискорень точки 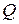 .
.
Значення прискорення т. С з відношення 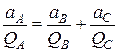 , а його напрям під кутом
, а його напрям під кутом 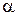 до
до 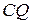 згідно напряму
згідно напряму 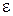 .
.
Випадок VІ. У даний момент часу відомі модулі і напрям прискорень двох точок 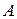 і
і 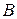 твердого тіла. При чому вектори
твердого тіла. При чому вектори 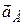 і
і 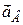 паралельні (рис. 18.12). Положення МЦП у цьому випадку визначається на підставі того, що модулі прискорень точок пропорційні довжинам відрізків, що з’єднують точки з МЦП і кут між векторами прискорення точок і цими відрізками сталий:
паралельні (рис. 18.12). Положення МЦП у цьому випадку визначається на підставі того, що модулі прискорень точок пропорційні довжинам відрізків, що з’єднують точки з МЦП і кут між векторами прискорення точок і цими відрізками сталий:
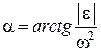
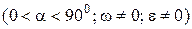 .
.
На рис. 18.13 зображено визначення МЦП при 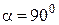 і якщо
і якщо 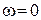 , а
, а 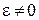 .
.
На рис. 18.14 зображено визначення МЦП при 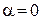 і якщо
і якщо 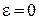 ,
, 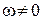 .
.
Випадок VІІ. Якщо прискорення двох точок тіла 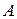 і
і 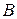 рівні за модулем івектори
рівні за модулем івектори 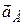 і
і 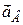 паралельні, то МЦП перебуває у нескінченності, а прискоренняусіх точок тіла рівні між собою.
паралельні, то МЦП перебуває у нескінченності, а прискоренняусіх точок тіла рівні між собою.
 |
 |
18.5. Приклади розв’язання задач
Приклад 1. Знайти прискорення точки 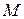 на ободі колеса радіусом
на ободі колеса радіусом 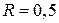 , що котиться без ковзання по нерухомій рейці швидкістю
, що котиться без ковзання по нерухомій рейці швидкістю 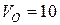 м/с і прискоренням
м/с і прискоренням 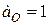 м/с
м/с 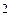 (рис. 18.15).
(рис. 18.15).
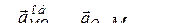 Розв’язання. Рух колеса є плоскопаралельним (
Розв’язання. Рух колеса є плоскопаралельним ( 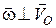 ). Миттєва вісь обертання проходить через миттєвий центр швидкостей
). Миттєва вісь обертання проходить через миттєвий центр швидкостей 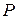 (
( 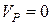 ), перпендикулярно рисунку. За полюс обираємо центр колеса
), перпендикулярно рисунку. За полюс обираємо центр колеса 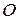 відповідно формулі (18.6), маємо:
відповідно формулі (18.6), маємо:
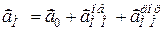 ;
;
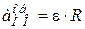 ;
; 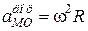 .
.
Знайдемо 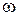 і
і 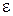 :
:
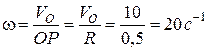 ;
;
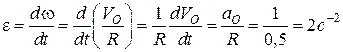 .
.
Тоді величина прискорення точки 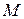 дорівнюватиме:
дорівнюватиме:
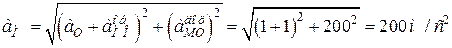 .
.
Приклад 2. Знайти положення миттєвого центра прискорень колеса радіусом 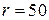 cм, що котиться без ковзання по нерухомій рейці зі швидкістю
cм, що котиться без ковзання по нерухомій рейці зі швидкістю 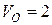 м/с і прискоренням
м/с і прискоренням 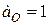 м/с
м/с 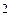 . Визначити напрям прискорення МЦШ (рис. 16.16).
. Визначити напрям прискорення МЦШ (рис. 16.16).
 Розв’язання. За полюс обираємо центр колеса
Розв’язання. За полюс обираємо центр колеса 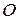 . Тодіточка
. Тодіточка 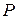 – МЦШ, тобто
– МЦШ, тобто
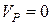 ;
; 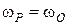 ;
; 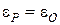 ;
;
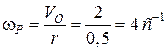 ;
;
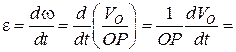
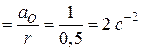 .
.
Оскільки, 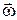 і
і 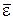 направлені в один бік, то
направлені в один бік, то 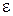 >0. Для визначення положення миттєвого центра прискорень точки
>0. Для визначення положення миттєвого центра прискорень точки 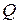 слід повернути напрямок вектора
слід повернути напрямок вектора 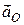 на кут
на кут 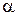 у бік прискореного обертання, тобто за годинниковою стрілкою, і відкласти на одержаному промені відрізок
у бік прискореного обертання, тобто за годинниковою стрілкою, і відкласти на одержаному промені відрізок
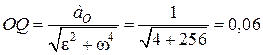 м
м 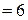 см.
см.
Зазначимо, що
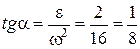 ,
, 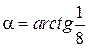 .
.
звідки 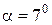 . Відмічаємо точку
. Відмічаємо точку 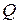 на рисунку.
на рисунку.
Прискорення МЦШ за модулем дорівнює 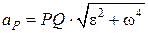 , де
, де 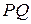 – замірюємо лінійкою з урахуванням масштабу. Вектор прискорення
– замірюємо лінійкою з урахуванням масштабу. Вектор прискорення 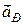 , спрямований під кутом
, спрямований під кутом 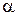 , який відкладемо від відрізка
, який відкладемо від відрізка 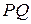 проти обертання колеса.
проти обертання колеса.
Дата добавления: 2014-12-20; просмотров: 2277;
