Прискорення будь-якої точки плоскої фігури дорівнює геометричній сумі прискорення полюса, а також доцентрового і обертального прискорення цієї точки відносно полюса.

Для доведення цієї теореми згадаємо, що рух плоскої фігури в її площині є складним, який складається з поступального руху разом з довільно взятим полюсом і обертального навколо полюса.

Будемо виходити з формули для швидкості будь-якої точки 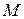плоскої фігури:

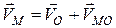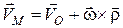, , (18.1)

тут 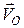– швидкість полюса 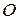, 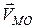- швидкість т.М в обертальному русі відносно полюса О, 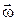– кутова швидкість плоскої фігури; 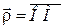– радіус-вектор точки 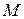відносно полюса О (рис. 18.1).

Продиференціюємо рівність (18.1) за часом:

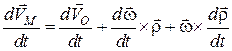. (18.2)

Тут

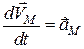– прискорення точки

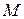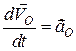- прискорення полюса О,

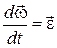– вектор кутового прискорення плоскої фігури, направлений так само як і

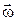, якщо

;

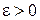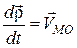– швидкість точки

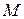в обертальному русі навколо полюса

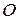(рис. 18.2).

Отже, рівняння (18.2), з урахуванням вище означеного, набуває вигляду:

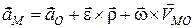. (18.3)

Другий і третій доданки в рівності (16.3) відповідно є обертальне і доцентрове прискорення точки 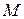у обертальному русі навколо полюса:

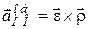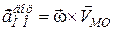; . (18.4)

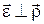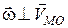Оскільки , а , то за величиною прискорення (18.4) дорівнюють:

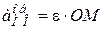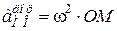; . (18.5)

Напрями 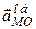і 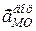можна визначити за правилом векторного добутку. Обертальне прискорення направлене перпендикулярно до 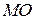у бік обертання, якщо 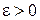, і в протилежний бік, якщо 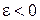. Доцентрове прискорення направлене за 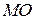до полюса 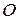(рис. 18.2).

Остаточно, з урахуванням (16.4), прискорення довільної точки плоскої фігури дорівнює:

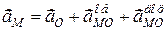. (18.6)

Теорему доведено.

Зауважимо: векторна сума обертального і доцентрового прискорень є повним прискоренням точки 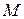у обертанні навколо полюса:

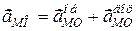. (18.7)

Тоді формула (18.6), яка виражає теорему про прискорення точок плоскої фігури, набуває вигляду

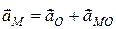. (18.8)

Отже, прискорення будь-якої точки 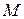плоскої фігури дорівнює геометричній сумі прискорення полюса і прискорення цієї точки в обертальному русі навколо полюса.

Модуль прискорення 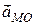точки 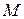в обертальному русі навколо полюса 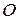з урахуванням того, що 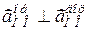, дорівнює

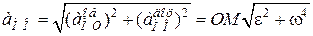. (18.9)

Кут 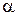між векторами 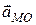і 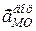визначається за його тангенсом (рис. 18.2):

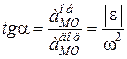. (18.10)

Цей кут для прискорень усіх точок плоскої фігури в даний момент часу однаковий, бо 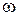і 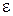є спільними для всіх точок плоскої фігури.

Відраховується кут 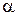від вектора 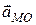у бік обертання плоскої фігури навколо полюса 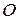, якщо обертання прискорене ( 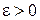), і в протилежний бік, якщо обертання плоскої фігури сповільнене ( ).

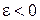Щоб розв'язувати задачі на визначення прискорень точок плоскої фігури, попередньо необхідно обчислити кутову швидкість 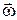, кутове прискорення 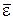і вибрати полюс 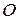. За полюс приймається та точка плоскої фігури, прискорення якої в даний момент відоме, або може бути знайдене з умов задачі. При розв’язанні задач на визначення прискорень точок, користуються або проектуванням рівності (18.6) на декартові осі або графічною побудовою.

18.2. Миттєвий центр прискорень (МЦП)

Миттєвим центром прискорень називається точка на площині, в якій рухається плоска фігура, прискорення якої стосовно до плоскої фігури в даний момент часу дорівнює нулю.

Ця точка позначається буквою .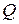

Нехай 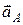прискорення точки 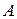плоскої фігури, кутова швидкість 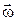і кутове прискорення 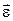задані за величиною і напрямом (рис. 18.3).

Для визначення положення миттєвого центру прискорень знаходимо 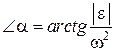. З точки А під кутом 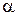до 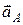, відкладеним у напрямку 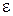, проводимо промінь 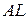, на якому відкладаємо відрізок 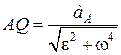. (18.11)

Одержана точка 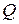є миттєвим центром прискорень, тобто .

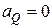Дійсно, приймаючи точку А за полюс, на підставі (18.8), маємо

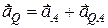, (18.12)

де, на підставі (18.9), за значенням

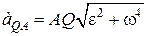. (18.13)

Вектор 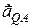складає з прямою 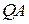той же кут 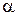, що і вектор 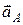з прямою 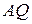, тобто вектори 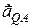і 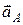прикладені у точці 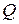, протилежні за напрямами. Після алгебраїчного додавання цих векторів, враховуючи (18.13) та (18.11), маємо:

.

<31 32 333435 36 37 >

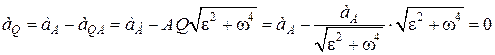Дата добавления: 2014-12-20; просмотров: 1786;