ВИЗНАЧЕННЯ ШВИДКОСТЕЙ ТОЧОК ПЛОСКОЇ ФІГУРИ ЗА ДОПОМОГОЮ МЦШ
17.1. Теорема про миттєвий центр швидкостей (МЦШ):
 При непоступальному русі плоскої фігури у своїй площині в кожний момент часу існує точка, швидкість якої по відношенню до плоскої фігури в цей момент часу дорівнює нулю.
При непоступальному русі плоскої фігури у своїй площині в кожний момент часу існує точка, швидкість якої по відношенню до плоскої фігури в цей момент часу дорівнює нулю.
Ця точка позначається літерою 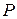 і називається миттєвим центром швидкостей (МЦШ). Під час руху плоскої фігури точка
і називається миттєвим центром швидкостей (МЦШ). Під час руху плоскої фігури точка  безперервно змінює своє положення.
безперервно змінює своє положення.
Отже, миттєвий центр швидкостей є точкою перетину миттєвої осі обертання з площиною руху.
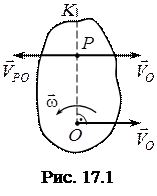
Уявімо собі плоску фігуру, яка рухається в своїй площині (рис. 17.1).
Припустимо, що в даний момент часу відома швидкість 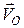 точки
точки 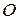 і кутова швидкість
і кутова швидкість 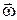 обертання плоскої фігури навколо точки
обертання плоскої фігури навколо точки 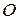 .
.
Візьмемо точку 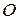 за полюс і знайдемо ту точку
за полюс і знайдемо ту точку 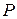 плоскої фігури, швидкість якої у даний момент часу дорівнює нулеві.
плоскої фігури, швидкість якої у даний момент часу дорівнює нулеві.
Для цього повернемо пряму, по якій направлений вектор 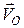 , на прямий кут у бік обертання плоскої фігури. На цій прямій
, на прямий кут у бік обертання плоскої фігури. На цій прямій 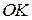 на відстані
на відстані 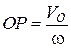 від полюса визначимо точку
від полюса визначимо точку 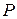 . Використовуючи
. Використовуючи 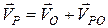 ,
,
знайдемо швидкість точки 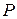 . Причому швидкість
. Причому швидкість 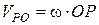 і спрямована перпендикулярно
і спрямована перпендикулярно 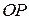 у бік обертання. Отже, швидкість
у бік обертання. Отже, швидкість 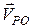 в обертальному русі точки
в обертальному русі точки 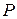 навколо полюса
навколо полюса 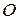 спрямована в протилежний бік швидкості
спрямована в протилежний бік швидкості 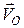 полюса
полюса 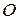 , перенесеної в точку
, перенесеної в точку 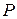 .
.
Тоді ці вектори, що діють по одній прямій, додаються алгебраїчно:
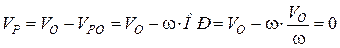 , тобто
, тобто 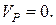
Отже, доведено, що миттєвий центр швидкості плоскої фігури лежить на перпендикулярі до швидкості 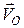 , на відстані
, на відстані 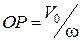 від полюса
від полюса 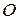 .
.
Миттєвий центр швидкості є єдиною точкою плоскої фігури для даного моменту часу. В інший момент часу миттєвим центром швидкості для неї буде вже інша точка.
Наслідок І. Якщо прийняти миттєвий центр швидкостей за полюс, то рух плоскої фігури в даний момент часу можна розглядати як обертальний навколо миттєвої осі, яка перпендикулярна до плоскої фігури і проходить через миттєвий центр швидкості (МЦШ).
Припустимо, що миттєвий центр швидкостей 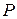 відомий. Тоді, прийнявши точку
відомий. Тоді, прийнявши точку 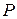 за полюс і враховуючи, що в цьому випадку швидкість його
за полюс і враховуючи, що в цьому випадку швидкість його 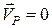 , знайдемо швидкість довільної точки
, знайдемо швидкість довільної точки 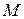 :
:
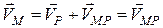 , (17.1)
, (17.1)
Тут 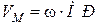 і спрямований вектор
і спрямований вектор 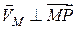 у бік обертання.
у бік обертання.
Для будь-якої іншої точки  можна записати аналогічно:
можна записати аналогічно:
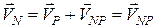 , (17.2)
, (17.2)
Тут 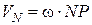 і спрямований вектор
і спрямований вектор 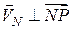 у бік обертання.
у бік обертання.
Наслідок ІІ. Швидкості точок плоскої фігури пропорційні відстаням до миттєвого центру швидкостей і направлені перпендикулярно до відрізків, які з'єднують ці точки з миттєвим центром швидкостей, у бік обертання плоскої фігури
З формул (17.1) і (17.2), які визначають абсолютне значення швидкостей точок плоскої фігури, виходить що:
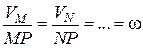 . (17.3)
. (17.3)
Отже, швидкості точок плоскої фігури розподіляються пропорційно відстаням цих точок до миттєвого центра швидкостей.
Дата добавления: 2014-12-20; просмотров: 2487;
