Швидкість довільної точки плоскої фігури дорівнює векторній сумі швидкості полюса і швидкості цієї точки у обертальному русі навколо полюса.

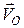Рух плоскої фігури в її площині є складним, який складається з поступального руху зі швидкістю полюса 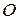(рис. 16.4) і обертального руху навколо цього полюса з кутовою швидкістю .

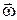Візьмемо будь-яку точку 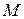плоскої фігури (рис. 16.4). Положення цієї точки відносно початку нерухомих осей 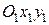визначається з 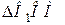радіусом-вектором

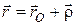, (16.2)

де 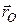та 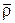– відповідно радіус-вектор полюса 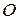та радіус-вектор точки 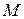відносно полюса .

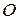Швидкість точки 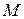, враховуючи (16.2), дорівнює:

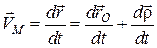. (16.3)

Тут 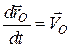– швидкість полюс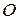а , а 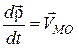– швидкість точки 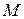в обертальному русі плоскої фігури навколо полюса .

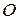Тоді рівність (16.3) приймає такий вигляд:

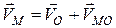. (16.4)

За формулою Ейлера швидкість точки 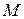у обертальному русі плоскої фігури відносно центра 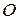можна подати у вигляді векторного добутку вектора кутової швидкості 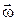плоскої фігури на радіус вектор 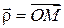, тобто:

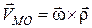. (16.5)

Вектор 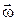направлений перпендикулярно до плоскої фігури і проходить через полюс .

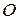Тому за модулем 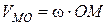, а за напрямком вектор 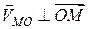і спрямований у бік обертання.

З урахуванням (16.5), вектор швидкості довільної точки М дорівнює:

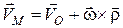. (16.6)

Таким чином, вектор лінійної швидкості 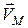будь-якої точки М плоскої фігури зображується діагоналлю паралелограма, побудованого на векторі швидкості полюса 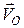перенесеного у точку 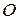, і векторі швидкості 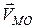в обертальному русі точки 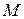навколо полюса 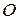(рис. 16.4).

16.4. Теорема про проекції швидкостей двох точок плоскої фігури: