Приклад розв’язування задачі
Приклад. Ексцентрик (рис. 15.2) обертається навколо осі, що перпендикулярна площині креслення, за законом:
 рад.
рад.
Визначити швидкість і прискорення точки 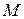 ексцентрика у момент
ексцентрика у момент  сек, якщо
сек, якщо 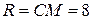 см і
см і  см.
см.
 Розв’язання. Кутова швидкість та кутове прискорення ексцентрика змінюються за закономами:
Розв’язання. Кутова швидкість та кутове прискорення ексцентрика змінюються за закономами:
 ;
; 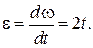
Якщо  сек, то
сек, то 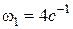 ,
, 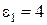 сек
сек 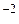 .
.
Швидкість точки у цей момент дорівнює:
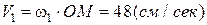 .
.
і направлена перпендикулярно ОМ у бік обертання (рис. 15.2).
Визначаємо обертальне (дотичне) та доцентрове (нормальне) прискорення точки 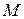 :
:
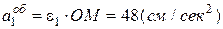 ;
; 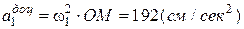 .
.
Модуль повного прискорення точки М:
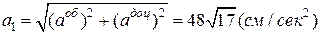 .
.
Вектор повного прискорення складає з 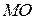 кут
кут 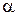 , причому
, причому
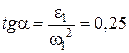 .
.
Дата добавления: 2014-12-20; просмотров: 1068;
