Швидкість точок тіла, що обертається навколо нерухомої осі
Згідно з натуральним способом визначення руху точки, алгебраїчне значення лінійної швидкості точки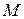 
дорівнює:
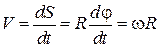. (15.3)
Отже, лінійна швидкість будь якої точки тіла, що обертається, дорівнює добутку кутової швидкості тіла на відстань точки від осі обертання. Вектор цієї швидкості, направлений за дотичною до кола, яке описує точка, у бік обертання, тобто перпендикулярно до радіуса кола.
Формулу (15.3) можна представити як векторний добуток двох векторів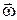 
і 
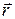, врахувавшиз 
, що 
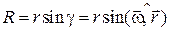, де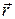 
– радіус-вектор точки відносно точки О (рис. 15.3). Тоді за модулем швидкість точки дорівнює:
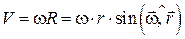. (15.4)
Спрямований вектор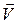 
перпендикулярно до площини, в якій лежать вектори 
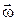і 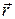, у той бік, звідки найкоротший перехід від 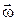до 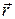видно як такий, що відбувається проти руху стрілки годинника.
Згадуючи, з математики векторний добуток двох векторів, приходимо до висновку, що
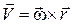. (15.5)
Дата добавления: 2014-12-20; просмотров: 1845;