Прискорення будь-якої точки тіла, що обертається навколо нерухомої осі, дорівнює векторній сумі обертального і доцентрового прискорень цієї точки.
Перша векторна складова, що дорівнює:
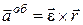 , (15.7)
, (15.7)
називається обертальним прискоренням.
Друга векторна складова, що дорівнює:
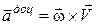 , (15.8)
, (15.8)
називається доцентровим (нормальним) прискоренням.
Знаходимо модуль і напрям цих складових прискорення точки.
Вектор обертального прискорення 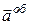 , у відповідності з (15.7), направлений від точки
, у відповідності з (15.7), направлений від точки 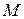 перпендикулярно до площини, що визначається векторами
перпендикулярно до площини, що визначається векторами 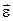 і
і 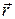 , тобто збігається з напрямом вектора швидкості точки, якщо
, тобто збігається з напрямом вектора швидкості точки, якщо 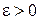 (рис. 15.1).
(рис. 15.1).
Числове значення обертального прискореннявизначається за формулою:
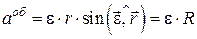 , (15.9)
, (15.9)
тобто дорівнює добутку кутового прискорення тіла на відстань точки М до осі обертання.
Вектор доцентрового прискорення 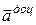 ,у відповідності з (15.8), направлений від точки
,у відповідності з (15.8), направлений від точки 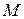 перпендикулярно до площини , що визначається вектором
перпендикулярно до площини , що визначається вектором 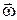 , перенесеним паралельно у точку
, перенесеним паралельно у точку 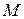 і вектором
і вектором 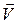 ,тобто спрямований вздовж радіуса
,тобто спрямований вздовж радіуса 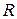 до осі
до осі 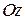 .
.
Числове значення доцентрового прискореннявизначається за формулою
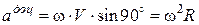 , (15.10)
, (15.10)
тобто дорівнює добутку квадрата кутової швидкості тіла на відстань точки 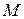 до осі обертання.
до осі обертання.
Модуль повного прискорення точки, з урахуванням того, що 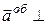
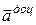 , дорівнює
, дорівнює
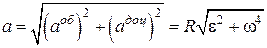 . (15.11)
. (15.11)
Кут 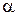 , утворений вектором повного прискорення
, утворений вектором повного прискорення 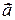 і вектором доцентрового прискорення
і вектором доцентрового прискорення 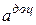 , визначається за формулою:
, визначається за формулою:
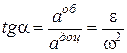 . (15.12)
. (15.12)
Дата добавления: 2014-12-20; просмотров: 1205;
