Абсолютна швидкість точки при складному русі дорівнює геометричній сумі відносної та переносної швидкостей.

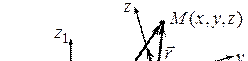Доведення. Нехай точка 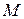рухається відносно рухомої системи координат 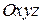, яка, в свою чергу, довільно рухається відносно умовно нерухомої системи 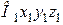(рис. 19.1).

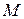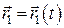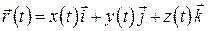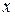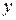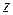Положення точки в абсолютному русі будемо визначати радіусом-вектором , а у відносному русі – радіусом-вектором , де , , координати точки у відносному русі, а 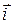, , 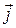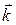– орти рухомих осей.

Якщо рухома система рухається не поступально, то орти 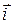, , 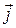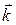змінюються за напрямом і тому також залежать від часу, тобто ; ; .

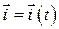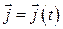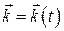З векторного 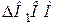(рис. 17.1), випливає, що:

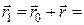
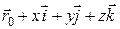. (19.1)

Тут 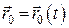– радіус-вектор точки 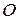, проведений з початку координат нерухомих осей .

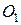Абсолютну швидкість точки 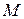знайдемо, диференціюючи рівність (19.1) за часом:

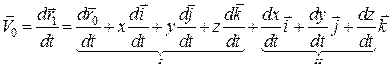. (19.2)

Поділимо доданки рівності (19.2) на групи І і ІІ та проаналізуємо їх

Якщо зупинити рухому систему, тобто вважати 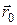і 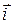, , 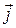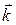– сталими, то перша група доданків (І) рівності (19.2) перетворюється на нуль.

Залишається друга група доданків (ІІ), що є швидкістю точки М відносно системи координат 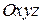, тобто відносною швидкістю точки:

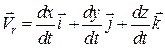. (19.3)

Якщо зупинити рух точки відносно рухомої системи координат, тобто вважати координати точки 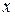, , 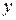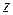– сталими, то друга група доданків рівності (19.2) перетворюється на нуль.

Залишається перша група доданків, що є швидкістю тієї точки 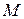рухомої системи, з якою в даний момент збігається точка 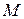, тобто її переносною швидкістю:

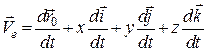. (19.4)

Формула (19.2), враховуючи позначення (19.3) та (19.4), остаточно набуває вигляду, що репрезентує доведену теорему:

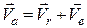. (19.5)

Отже, абсолютна швидкість 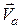точки 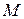при складному русі зображується діагоналлю паралелограма, побудованого на векторах її відносної 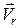і переносної 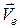швидкостей (рис. 19.1).

Модуль абсолютної швидкості точки можна визначити за формулою:

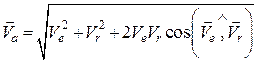. (19.6)

Виведені формули справедливі при будь-якому переносному русі.

19.3. Теорема Коріоліса про додавання прискорень: