Довільне переміщення плоскої фігури в її площині можна виконати сукупністю двох переміщень: поступального разом з довільно взятим полюсом і повороту навколо цього полюса.

Нехай плоска фігура перемістилась у своїй площині з положення І у положення ІІ так, що її відрізок 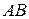зайняв положення 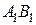(рис. 16.3).

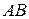З рисунку видно, що це переміщення можна провести так: перемістити плоску фігуру поступально, щоб відрізок зайняв паралельне йому положення 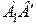, а потім повернути її навколо точки 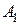на кут 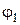. Або можна інакше перемістити плоску фігуру поступально так, щоб відрізок 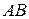зайняв паралельне положення 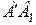, і повернути її навколо точки 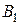на кут 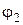. В першому випадку за полюс прийнято точку 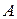, у другому – точку .

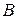Отже, поступальна частина переміщення плоскої фігури залежить від вибору полюса, а поворот від вибору полюса не залежить, бо .

Ми довели теорему для скінченого переміщення плоскої фігури. Аналогічно можна довести її і для нескінченно малого переміщення.

З цієї теореми виходить, що дійсний рух плоскої фігури в її площині в кожний момент часу можна розглядати як складний рух, що складається з двох рухів: поступального (переносного) разом з вибраним полюсом і обертального (відносного) навколо осі, що проходить через цей полюс.