Способи визначення положення миттєвого центру швидкостей. Центроїди.
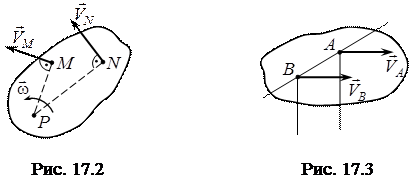
І. Якщо відомі напрямки швидкостей двох точок 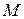 і
і 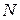 плоскої фігури, то миттєвий центр швидкостей точки
плоскої фігури, то миттєвий центр швидкостей точки 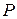 знаходиться у точці перетину перпендикулярів до
знаходиться у точці перетину перпендикулярів до 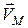 і
і 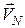 , проведених з цих точок (рис. 17.2).
, проведених з цих точок (рис. 17.2).
Зауважимо, якщо відоме положення МЦШ і задано модуль 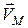 , то можна визначити кутову швидкість плоскої фігури, поділивши швидкість точки на її відстань до миттєвого центру швидкості
, то можна визначити кутову швидкість плоскої фігури, поділивши швидкість точки на її відстань до миттєвого центру швидкості 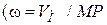 ), а далі легко визначити швидкість будь-якої точки N плоскої фігури (
), а далі легко визначити швидкість будь-якої точки N плоскої фігури ( 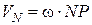 ).
).
 |
ІІ. Якщо швидкості
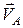 і
і  точок
точок  і
і 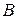 рівні і паралельні (рис. 17.3), то миттєвий центр швидкостей перебуває у нескінченності. Кутова швидкість плоскої фігури у даний момент дорівнює нулю. Плоска фігура в цьому випадку здійснює миттєво поступальний рух.
рівні і паралельні (рис. 17.3), то миттєвий центр швидкостей перебуває у нескінченності. Кутова швидкість плоскої фігури у даний момент дорівнює нулю. Плоска фігура в цьому випадку здійснює миттєво поступальний рух.
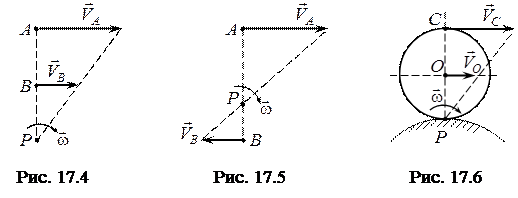 |
ІІІ. Якщо швидкості точок
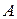 і
і  не дорівнюють одна одній за модулем і перпендикулярні до
не дорівнюють одна одній за модулем і перпендикулярні до 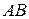 , то миттєвий центр швидкостей
, то миттєвий центр швидкостей 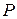 знаходиться у точці перетину прямої
знаходиться у точці перетину прямої 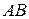 з прямою, яка з'єднує кінці векторів швидкостей
з прямою, яка з'єднує кінці векторів швидкостей 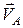 і
і 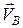 , (рис. 17.4) і (рис. 17.5). В цьому випадку для визначення миттєвого центра швидкостей, крім напряму, треба знати ще й модулі швидкостей
, (рис. 17.4) і (рис. 17.5). В цьому випадку для визначення миттєвого центра швидкостей, крім напряму, треба знати ще й модулі швидкостей 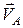 і
і 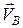 .
.
ІV. У разі кочення без ковзання рухомого контура плоскої фігури вздовж нерухомого, миттєвий центр швидкостей Р знаходиться у точці дотику цих контурів (рис. 17.6).
Вище розглянуті випадки знаходження миттєвого центра швидкостей (МЦШ) приводять до висновку:
Плоска фігура, що рухається в своїй площині, в кожний момент часу здійснює або миттєвообертальний, або миттєво поступальний рухи.
При плоскому русі, МЦШ безперервно змінює своє положення на площині. Цьому факту можна надати наочну геометричну інтерпретацію.
Попередньо зазначимо, що геометричне місце миттєвих центрів швидкостей називається центроїдою.
Оскільки при русі плоскої фігури МЦШ описує одну лінію в нерухомій системі координат, а другу в рухумій, то утворюються відповідно дві центроїди – нерухома і рухома.
Нерухома центроїда – це траєкторія МЦШ на нерухомій площині, а рухома– це траєкторія МЦШ на рухомій площині.
Так, при коченні колеса без ковзання по горизонтальній площині (рис. 17.6) нерухома центроїда – горизонтальна пряма, а рухома – коло.
В кожний момент часу рухома і нерухома центроїди мають загальну точку дотику 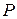 , швидкість якої дорівнює нулю, і яка є миттєвим центром швидкості.
, швидкість якої дорівнює нулю, і яка є миттєвим центром швидкості.
Тому, за теоремою Пуансо, плоский рух можна розглядати як кочення без ковзання рухомої центроїди по нерухомій.
План швидкостей точок плоскої фігури
План швидкостей – це графічне зображення (діаграма) векторів швидкостей точок плоскої фігури у фіксований момент часу її руху.
 Для побудови плана швидкостей потрібно знати величину і напрям швидкості однієї точки
Для побудови плана швидкостей потрібно знати величину і напрям швидкості однієї точки  , а також напрям швидкості якої-небудь іншої точки
, а також напрям швидкості якої-небудь іншої точки  плоскої фігури (рис. 17.6).
плоскої фігури (рис. 17.6).
Для визначення швидкості точки  виберемо полюс у точці
виберемо полюс у точці 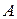 :
:
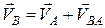 ,
,
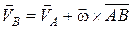 . (17.4)
. (17.4)
При русі плоскої фігури швидкість будь-якої її точки В визначається як геометрична сума швидкості полюса 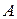 і швидкості
і швидкості 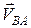 точки
точки 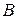 в обертальному русі плоскої фігури навколо полюса
в обертальному русі плоскої фігури навколо полюса 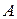 . При цьому
. При цьому 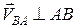 .
.
Для побудови вектора 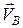 , згідно з (17.4), вибираємо поза контуром плоскої фігури довільну точку
, згідно з (17.4), вибираємо поза контуром плоскої фігури довільну точку 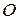 (полюс), з якої у вибраному масштабі відкладаємо вектор
(полюс), з якої у вибраному масштабі відкладаємо вектор 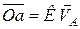 , де
, де 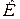 – масштабний коефіцієнт (рис. 17.3).
– масштабний коефіцієнт (рис. 17.3).
З кінця цього вектора, тобто з точки а, проводимо пряму 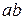 , перпендикулярно до
, перпендикулярно до 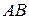 (
( 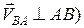 , до перетину її в точці
, до перетину її в точці 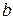 з прямою, проведеною з полюса
з прямою, проведеною з полюса 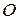 паралельно напряму шуканої швидкості точки
паралельно напряму шуканої швидкості точки 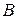 . Вектор
. Вектор 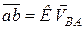 є у вибраному масштабі швидкістю точки
є у вибраному масштабі швидкістю точки 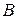 при обертальному русі плоскої фігури навколо точки
при обертальному русі плоскої фігури навколо точки 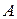 , а вектор
, а вектор 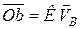 .
.
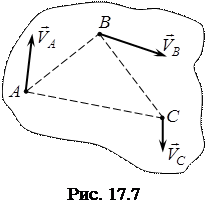
 Переходимо до побудови вектора швидкості
Переходимо до побудови вектора швидкості 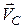 точки
точки 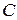 , яка поки що невідома ні за значенням, ні за напрямком. Аналогічно (17.4), запишемо, що з одного боку
, яка поки що невідома ні за значенням, ні за напрямком. Аналогічно (17.4), запишемо, що з одного боку 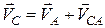 , а з іншого
, а з іншого 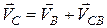 . Напрям вектора
. Напрям вектора 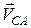 знайдемо, якщо через точку
знайдемо, якщо через точку 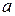 плану швидкостей (рис. 17.8) проведемо пряму
плану швидкостей (рис. 17.8) проведемо пряму 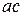 перпендикулярно до
перпендикулярно до 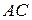 (рис. 17.7). Напрям вектора
(рис. 17.7). Напрям вектора 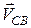 знайдемо, якщо через точку
знайдемо, якщо через точку 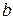 плану швидкостей проведемо пряму
плану швидкостей проведемо пряму 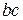 , перпендикулярну до
, перпендикулярну до 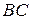 . Точка с плану швидкостей є точкою перетину прямих
. Точка с плану швидкостей є точкою перетину прямих 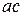 і
і 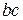 . Вектор
. Вектор 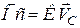 дорівнює у відповідному масштабі швидкості точки
дорівнює у відповідному масштабі швидкості точки 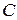 плоскої фігури. Вектор
плоскої фігури. Вектор 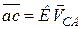 і вектор
і вектор 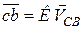 .
.
Дата добавления: 2014-12-20; просмотров: 4065;
