Визначення булевої функції
Визначення 4.1. Булевою функцією f(x1, x2, ... , xn) називається довільна функція n змінних, аргументи якої x1, x2, ... , xn і сама функція f приймає значення 0 або 1, тобто xi 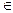 {0, 1}, i = 1, 2, ... , n; f(x1, x2, ... , xn)
{0, 1}, i = 1, 2, ... , n; f(x1, x2, ... , xn) 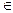 {0, 1}.
{0, 1}.
Будь-яка булева функція може бути представлена таблицею, у лівій частині якої перераховані всі набори змінних (їх 2n), а в правій частині – значення функції. Приклад такого завдання представлений у таблиці 4.1.
Таблиця 4.1
| x1 x2 x3 | f(x1, x2, x3) |
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
Для формування стовпця значень змінних зручний лексико-графічний порядок, відповідно до якого кожен наступний набір значень виходить із попереднім додатком 1 у двійковій системі числення, наприклад, 100 = 011+ 1.
Всього існує 22 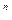 різних булевих функцій n змінних.
різних булевих функцій n змінних.
Функцій однієї змінної – 4. З них виділимо функцію “заперечення x”(позначається Øx). Ця функція представлена в таблиці 4.2.
 Таблиця 4.2
Таблиця 4.2
| x | Øx |
Булевих функцій двох змінних – 16 (22 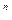 при n = 2). Ті з них, які мають спеціальні назви, представлені в таблиці 4.3.
при n = 2). Ті з них, які мають спеціальні назви, представлені в таблиці 4.3.
Таблиця 4.3
| x1 x2 | x1Vx2 | x1& x2 | x1 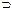 x2 x2
| x1~x2 | x1 Å x2 | x1¯ x2 | x1ï x2 |
| 0 0 0 1 1 0 1 1 | 0 | 1 | 1 |
У таблиці 4.3 представлені наступні функції двох змінних:
x1Vx2 – диз’юнкція;
x1& x2 – кон’юнкція;
x1Éx2 – імплікація;
x1~x2 – еквівалентність;
x1Å x2 – додавання по модулі 2;
x1¯x2 – стрілка Пірса;
x1ï x2 – штрих Шеффера.
Інші функції спеціальних назв не мають і можуть бути виражені через перераховані вище функції.
Дата добавления: 2014-12-22; просмотров: 1938;
