Формули логіки булевих функцій
Визначення 4.1.2. Формула логіки булевих функцій визначається індуктивно в такий спосіб:
1. Будь-яка змінна, а також константи 0 й 1 є формула.
2. Якщо A й B – формули, то ØA, AVB, A&B, A É B, A ~ B є формули.
3. Ніщо, крім зазначеного в пунктах 1-2, не є формула.
Приклад 4.1.
Вираз (ØxVy)&((y É z) ~ x) є формулою. Вираз Øx&y É z Ø ~x не є формулою. Частина формули, що сама є формулою, називається підформулою.
Приклад 4.2.
x&(y Éz) – формула; y Éz – її підформула.
Визначення 4.1.3. Функція f є суперпозиція функцій f1, f2, ... , fn якщо f виходить за допомогою підстановок цих формул одна в одну і перейменуванням змінних.
Приклад 4.3.
f1 = x1&x2 (кон’юнкція); f2 = Øx (заперечення).
Можливі дві суперпозиції:
1) f = f1(f2) = (Øx1)&(Øx2)– кон’юнкція заперечень;
2) f = f2(f1) = Ø(x1&x2) – заперечення кон’юнкцї.
Порядок підстановки задається формулою.
Усяка формула задає спосіб обчислення функції, якщо відомі значення змінних.
Приклад 4.4.
Побудуємо таблицю значень функції f(x1, x2, x3) = Ø(x2 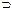 Øx3) ~ (Øx1Vx2).
Øx3) ~ (Øx1Vx2).
Таблиця 4.4 представляє послідовне обчислення цієї функції.
Таблиця 4.4
| x1 x2 x3 | Øx3 | x2 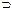 Øx3 Øx3
| Ø(x2 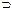 Øx3) Øx3)
| Øx1 | Øx1Vx2 | f(x1, x2, x3) |
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
Таким чином, формула кожному набору аргументів ставить у відповідність значення функції. Отже, формула так само, як і таблиця, може служити способом Задача функції. Надалі формулу будемо ототожнювати з функцією, що вона реалізує. Послідовність обчислень функції задається дужками. Прийнято угоду про опускання дужок у відповідності з наступною пріоритетністю операцій: Ø, &, V, É і ~.
Дата добавления: 2014-12-22; просмотров: 1321;
