Означення поля. Приклади полів
У кожному кільці для операції додавання здійсненна обернена операція – віднімання. Про обернену до операції множення – ділення – в означенні кільця не йдеться.
Слід зауважити, що ділення на нуль неможливе у жодній з числових множин. Ця властивість має місце і в абстрактних кільцях – не можна ділити на нульовий елемент q.
Важливу роль в математиці відіграють комутативні кільця, в яких здійсненна операція ділення (крім ділення на нуль). Їх називають полями.
Означення 3.3.1. Комутативне кільце Р називають полем, якщо воно має принаймні один елемент, відмінний від нульового і якщо в ньому в усіх випадках здійсненна операція ділення, крім ділення на нуль, тобтоякщо для довільних елементів кільця а і b, а¹q у кільці міститься, і при тому єдиний, такий елемент q, для якого a×q=b.
Елемент q називають часткою елементів а і b і записують 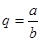 .
.
Аналогічно означують і числові поля. Існують ще й інші означення поля.
Означення 3.3.2. Комутативне кільце Р з одиницею, яке воно має принаймні один елемент, відмінний від нульового, називають полем, якщо для його кожного елемента а, а¹q існує єдиний обернений елемент а-1, такий що a× а-1=е.
Означення 3.3.3. Комутативне кільце Р, в якому існує хоча б один елемент, відмінний від нульового, називають полем, якщо сукупність його елементів без q утворює групу відносно операції множення.
Приклади полів.
1. Множини всіх раціональних, дійсних і комплексних чисел Q, R, C є полями.
2. Множина чисел виду 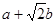 , де а і b – раціональні числа, є полем.
, де а і b – раціональні числа, є полем.
Доведення
Доведемо, що результати операцій додавання, віднімання, множення і ділення належать також до чисел виду 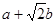 . Для цього візьмемо два різних числа заданого виду
. Для цього візьмемо два різних числа заданого виду 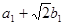 і
і  .
.
1) Операції додавання і віднімання: 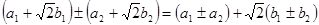 .
.
Тут роль a відіграє вираз  , який сумою (різницею) двох раціональних чисел
, який сумою (різницею) двох раціональних чисел 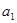 і
і 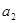 , а тому і раціональним числом, а роль b – вираз
, а тому і раціональним числом, а роль b – вираз  , що є також раціональним числом з аналогічних міркувань.
, що є також раціональним числом з аналогічних міркувань.
2) Операція множення:
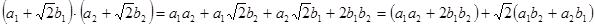 .
.
Тут у ролі a виступає вираз 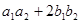 , а роль b – вираз
, а роль b – вираз 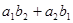 , що є раціональними числами, отриманими в результаті додавання множення раціональних чисел
, що є раціональними числами, отриманими в результаті додавання множення раціональних чисел 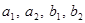 .
.
3) Операція ділення (для виділення чисел а і b позбудемося ірраціональності в знаменнику):
 .
.
Очевидно, що вирази 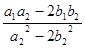 та
та 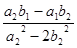 , щовиступають в ролі а і b, є раціональними, але викликає сумнів те, чи вони завжди мають зміст, тобто чи не дорівнює знаменник нулеві. Доведемо це від супротивного.
, щовиступають в ролі а і b, є раціональними, але викликає сумнів те, чи вони завжди мають зміст, тобто чи не дорівнює знаменник нулеві. Доведемо це від супротивного.
Припустимо, що 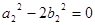 .
.
Звідси 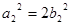 , або
, або 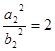 , або
, або  , або
, або  . Останній вираз є суперечністю, оскільки частка двох раціональних чисел не може бути числом ірраціональним. Твердження доведено.
. Останній вираз є суперечністю, оскільки частка двох раціональних чисел не може бути числом ірраціональним. Твердження доведено.
Дата добавления: 2014-12-22; просмотров: 1346;
