Вращение поля.

Приращение угловой функции θ(t) на всем отрезке [a,b], выраженное в единицах полного оборота, то есть величину

γ(Φ,Γ) = 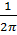(θ(b) − θ(a)) = 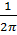θ(b), (1.11)

назовем вращением поля Φ на кривой Γ. Введение на кривой Γ параметра t превращает Γ в ориентированную кривую (перемещение точки при возрастании t задает эту ориентацию — см. рис. 1.2).

Приведенное выше определение вращения векторного поля зависит от способа введения параметра. Нетрудно видеть, что вращение поля Φ на кривой Γ при двух способах введения параметра одинаково, если эти параметры определяют на Γ одинаковую ориентацию. Если же две параметризации определяют разные ориентации, то вращения будут отличаться лишь знаком.

M(b)

Г

M(a)

Рис. 1.2

Таким образом, вращение поля определяется лишь ориентацией кривой.При переходе к противоположной ориентации абсолютная величина вращения сохраняется, а знак вращения меняется.

Из проведенных в предыдущем пункте рассуждений вытекает, что вращение не меняется при повороте всех векторов поля на один и тот же угол и при нормировании поля. Если ориентированная кривая Γ является объединением нескольких ориентированных кривых 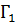, ,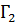..., 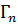(см. рис. 1.3), то вращение поля Φ на Γ равно сумме вращений на , ,..., .

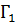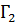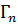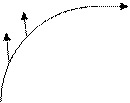
Рис. 1.3

Вращение может быть любым вещественным числом. Чтобы убедиться в этом, достаточно заметить, что θ(t) является угловой функцией поля

Φ(t) = (cosθ(t),sinθ(t)),(1.12)

рассматриваемого на отрезке

x = t, y = 0 (0 ≤ t ≤ 1);(1.13)

вращение γ этого поля равно 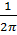θ(1)и может быть любым, так как непрерывная функция θ(t) может выбираться произвольным способом.

Если на двух концах кривой Γ векторы поля Φ направлены одинаково, то изменение угловой функции кратно 2π и, следовательно, вращение является целым числом. Аналогично, если на концах кривой Γ векторы поля Φ направлены противоположно, то γ(Φ,Γ) = n + , где n — некоторое целое число.

Вращение векторного поля параллельных векторов равно нулю, так как в этом случае θ(t) ≡ 0. Однако вращение может быть равно нулю и в других случаях.