Вращение векторного поля

1.1. Векторное поле.

Пусть в каждой точке M некоторого плоского множества Ω задан вектор Φ(M), лежащий в той же плоскости. В этом случае будем говорить, что на Ω задано векторное поле Φ. Если на плоскости определена некоторая прямоугольная система координат, то задание векторного поля Φ(M) эквивалентно заданию двух вещественных функций φ(M) и ψ(M) точки M ∈ Ω — компонент векторов Φ(M).

Векторное поле будем называть непрерывным, если функции φ(M), ψ(M) непрерывны.

Векторные поля встречаются и их приходится изучать при решении разнообразных математических задач.

В частности, во многих случаях векторы Φ(M) определяются как сдвиги точек, определяемые некоторым преобразованием A, заданным на Ω:

Φ(M) = A(M) − M.

В качестве второго примера рассмотрим систему дифференциальных уравнений

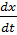= P(x,y), 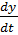= Q(x,y). (1.1)

Если решение этой системы рассматривать как закон движения точки в плоскости с прямоугольными координатами (x,y), то векторное поле

Φ(x,y) = (P(x,y),Q(x,y))(1.2)

— это поле скоростей движущихся по упомянутым законам точек. Выписать решения системы (1.1) в явном виде обычно невозможно, а общее представление о поле скоростей (1.2) в ряде случаев можно получить без труда. Априори ясно, что общие характеристики поля скоростей должны нести существенную информацию о решениях системы (1.1).

Рассмотрим, наконец, функцию f(z) комплексного переменного z = x + iy. Изучение функции

f(z) = u(x,y) + iv(x,y) (1.3)

равносильно изучению векторного поля

Φ(x,y) = (u(x,y),v(x,y)).(1.4)

1.2. Угловая функция.

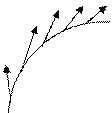
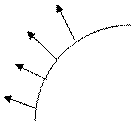
Пусть непрерывное векторное поле Φ(M) задано на некоторой жордановой кривой Γ без самопересечений. Если Γ — гладкая кривая, то примерами могут быть поля единичных касательных или нормальных векторов, направленных в определенную сторону (рис. 1.1).

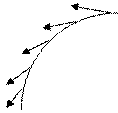Рис. 1.1

Допустим, что кривая Γ задана в параметрической форме:

x = x(t), y = y(t) (a ≤ t ≤ b).(1.5)

Тогда задание векторного поля

Φ(x,y) = (φ(x,y),ψ(x,y))(1.6)

на кривой Γ равносильно заданию вектор-функции

Φ(t) = (φ(x(t),y(t)),ψ(x(t),y(t))) (1.7)

на отрезке [a,b].

Пусть вектор-функция Φ(t) непрерывна и все векторы Φ(t) не равны нулю. Определим для каждого t ∈ [a,b] угол (в радианах) между векторами Φ(t) и Φ(a), отсчитанный от Φ(a) в положительном направлении (против хода часовой стрелки). Этот угол является многозначной функцией t. Через θ(t) обозначим непрерывную ветвь этой функции, обращающуюся в нуль приt = a, и назовем ее угловой функцией поля Φ на кривой Γ.

В качестве примера рассмотрим векторное поле

Φ(x,y) = (x,y) (1.8)

на кривой (половине единичной окружности)

x = cosπt, y = sinπt (0 ≤ t ≤ 1).(1.9)

Очевидно (рассмотрите чертеж), θ(t) = πt.

Из определения угловой функции вытекает, что она не меняется, если все векторы поля поворачивать на один и тот же угол. Угловая функция не изменится при замене каждого вектора Φ(x,y) единичным вектором того же направления, то есть при переходе к “нормированному” полю

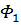(x,y) = 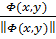(1.10)

(через 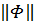здесь и ниже обозначается длина вектора Φ). Формула (1.10) имеет смысл, так как угловая функция определена лишь для полей, не имеющих нулевых векторов.

В заключение пункта подчеркнем, что угловая функция зависит от того, каким способом на кривой Γ введен параметр.