Циркуляция

Циркуля́цией ве́кторного по́ля называется криволинейный интеграл второго рода, взятый по произвольному замкнутому контуру Γ. По определению.

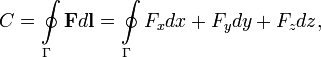
Где 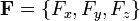- векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур Γ, 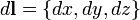- бесконечно малое приращение радиус-вектора 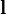вдоль контура. Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру. Приведенное выше определение справедливо для трёхмерного случая, но оно, как и основные свойства, перечисленные ниже, прямо обобщается на произвольную размерность пространства.

Аддитивность:

Циркуляция по контуру, ограничивающему несколько смежных поверхностей, равна сумме циркуляций по контурам, ограничивающим каждую поверхность в отдельности, то есть

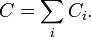
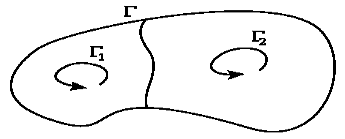
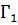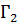Свойство аддитивности циркуляции: циркуляция по контуру Γ есть сумма циркуляций по контурам и , то есть C = +

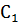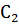
Формула Стокса:

Циркуляция вектора F по произвольному контуру Г равна потоку вектора 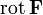через произвольную поверхность S, ограниченную данным контуром.

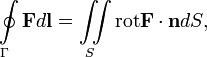
Где

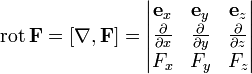
Ротор вектора F.

В случае, если контур плоский, например лежит в плоскости OXY, справедлива теорема Грина

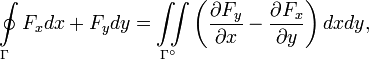
Где 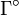- плоскость, ограничиваемая контуром Γ (внутренность контур).