Дивергенция векторного поля

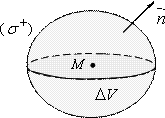
Дивергенция (или расходимость) векторного поля 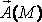в точке М - это предел отношения потока вектора 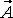через замкнутую поверхность 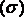окружающую точку М, в направлении ее внешней нормали к объему, ограниченному этой поверхностью, при условии, что вся поверхность 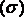, стягивается в точку М:

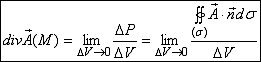(1)

Основные свойства дивергенции:

1. 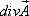- это дифференциальная характеристика поля, является скалярной величиной.

2.В каждой точке М поля 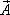показывает наличие источников или стоков поля:

3. если 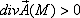, то в точке М есть источник поля 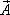, при этом значение 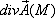численно равно мощности источника;

4. если , то в точке М есть сток поля 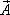при этом значение 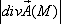численно равно мощности стока;

5. если 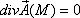, то в точке М нет ни источника, ни стока поля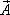

6. 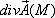вычисляется по формуле:

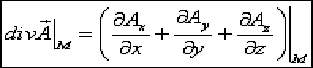
Воспользуемся формулой Остроградского-Гаусса, связывающей интеграл по замкнутой поверхности с интегралом по объёму, ограниченному этой поверхностью:

Применяем теорему о среднем к тройному интегралу:

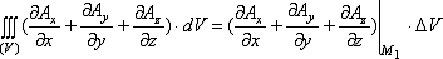
где 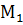- это некоторая фиксированная точка в объёме, ограниченном замкнутой поверхностью (σ),

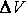-величина этого объёма.

Теперь используем определение (1) дивергенции:

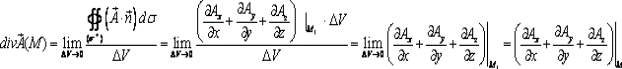
Так как при 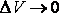точка 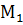стремится к точке M.

Если использовать понятие дивергенции, то теорема Остроградского-Гаусса в векторной форме:

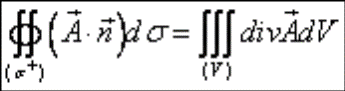
то есть поток вектора 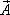изнутри замкнутой поверхности 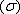равен тройному интегралу от дивергенции вектора 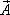по объему, ограниченному этой поверхностью.

Так как 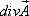можно рассматривать как плотность распределения источников и стоков векторного поля 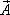то тройной интеграл

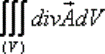
равен суммарной мощности источников и стоков по объему .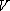

Учитывая это, смысл теоремы Остроградского-Гаусса в форме (3) можно сформулировать следующим образом: поток векторного поля 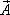изнутри замкнутой поверхности 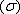равен суммарной мощности источников и стоков этого поля, заключенных в объеме 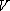, ограниченном этой поверхностью .

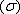Следовательно, если поток равен 0, то внутри поверхности 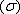нет источников и стоков поля 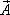или они уравновешивают друг друга.

Линейность дивергенции:

Это следует из линейности операций сложения векторов и дифференцирования.

Дивергенция произведения скалярного поля 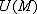на векторное поле 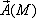вычисляется по формуле:

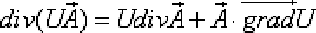
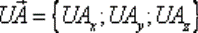
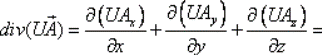
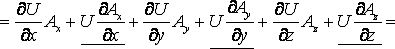
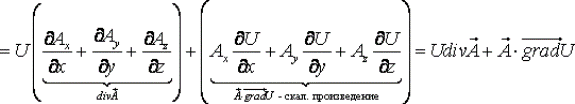
Примеры 1 (вычисление дивергенции векторного поля)

Дано 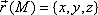- поле радиус-вектора точки 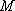. Вычислить

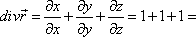Решение 3

то есть каждая точка М этого поля является источником постоянной мощности, равной 3.

Вычислить 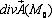и объяснить смысл ее значения, если

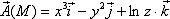
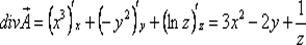Решение

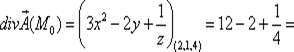10,25

Значение 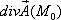указывает на то, что в заданной точке есть источник векторного поля 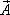и мощность этого источника равна 10,25.

По рассмотренному примеру можно заметить, что любое векторное поле 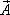сопровождается скалярным полем 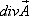его дивергенций.