Формулы Стокса

Формула Стокса устанавливает связь между поверхностным и криволинейным интегралами, а также обобщает формулу Грина а пространственный случай. Т: Пусть функции P(x,y,z), Q(x,y,z), R(x,y,z) непрерывны вместе со своими частными производными на гладкой ориентированной поверхности G, ограниченной гладкой замкнутой кривой L. Тогда

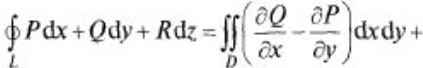
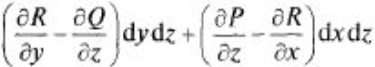
Эта формула называется формулой Стокса.

Если сторона поверхности выбрана, то направление обхода контура L берется положительным, т.е. таким, что при обходе контура по выбранной стороне поверхности:

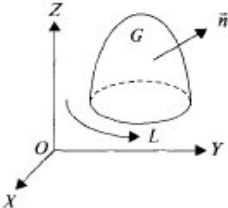
Из формулы Стокса следует, что если

то криволинейный интеграл по любой пространственной замкнутой кривой L равен нулю:

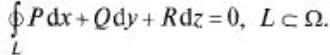
Как и в случае плоской кривой 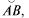условия являются необходимыми и достаточными для независимости криволинейного 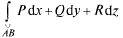от пути интегрирования. При их выполнении подынтегральное выражение - полный дифференциал некоторой функции

u(x,y,z): Pdx+ Qdy+ Rdz = du,

Заключение

Для того что бы сделать вывод о проделанной работе обратимся к задачам, которые были поставлены в введении.

Итак, примерами векторных полей служат силовое поле (поле тяготения, электрическое и электромагнитное поля) и поле скоростей текущей жидкости. Векторное поле задано, если в каждой точке Р поля указан соответствующий этой точке вектор А(Р).

Дивергенцией, или расходимостью, векторного поля А(Р) в точке Р называется предел отношения потока вектора через поверхность, окружающую точку Р, к объему, ограниченному этой поверхностью, при условии, что вся поверхность стягивается в точку Р.

Циркуляцией вектора А(Р) вдоль замкнутого контура L называется криволинейный интеграл по этому контуру от скалярного произведения вектора А(Р) на вектор dS касательной к контуру.

По результатам курсовой работы можно сделать вывод, что с помощью векторного анализа можно описать поведение любого поля, в любой точке пространства пользуясь рядом характеристик, таких как, дивергенция, циркуляция , поток , ротор.

Литература

1. М.А. Красносельский, А.И. Перов, А.И. Поволоцкий, П.П. Зайбеко, «Векторные поля на плоскости» М.,Государственное издательство физико-математической литературы 1963 г.

2. Мышкис «Лекции по высшей математике».

3. Данко П.Е., Попов А.Г., Кожевников Т.Я., «Высшая математика в упражнениях и задачах» М., Выс.школа 1980 г.

4. Красносельский М.А. «Топологические методы в теории нелинейных интегральных уравнений.», М.: Гостехиздат, 1956 г.