Дифференциальные уравнения движения Эйлера и Навье – Стокса

Зависимость между силами, действующими в жидкости, устанавливается в форме уравнений движения. Баланс действующих в потоке сил выражается в случае движения идеальной жидкости уравнениями Эйлера, в случае движения идеальной (вязкой) жидкости – уравнениями Навье-Стокса.

Рассмотрим общий случай – неустановившегося движения вязкой несжимаемой 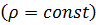жидкости.

Выделим в потоке элементарный параллелепипед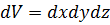

На элемент жидкости действует:

1. Сила тяжести

2. Поверхностные силы:

- Нормальные давление

- Касательные трение

При равновесии касательные силы равны нулю

Рассмотрим проекции сил тяжести и давления.

На ось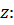

Сила тяжести: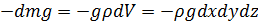

Сила давления:

- На нижнюю грань:

- На верхнюю грань: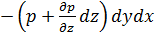

Сумма равна:

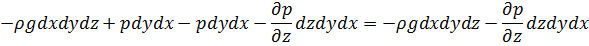
На ось

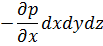
На ось

Для учета сил вязкости рассмотрим одномерное движение в направлении оси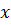

Действие сил трения проявляется в возникновении касательных напряжений 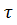(силе трения на единицу поверхности) на поверхности верхней и нижней граней.

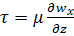уравнение Ньютона

Направление касательных сил ( ):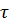

Более быстрые вышележащие слои «разгоняют» параллелепипед, а более медленные нижележащие слои «затормаживают» его.

Проекция равнодействующих сил трения на ось

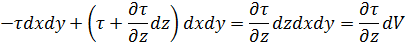
Подставим значение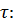

Для трехмерного потока составляющая скорости будет меняться по всем трем осям координат:

Проекция на ось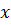

Сумма частных вторых производных по осям координат – оператор Лапласа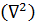

Следовательно:

на ось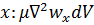

на ось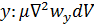

на ось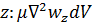

В соответствии с основным принципом динамики сумма проекций сил на оси координат равна произведению массы жидкости на проекции ускорения на оси координат:

масса

ускорение для неустановившегося потока полная (субстанциональная) производная скорости по времени:

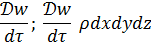
Сокращая на :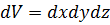

на ось

на ось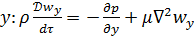

на ось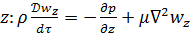

Это уравнение Навье-Стокса, описывающее движение вязкой несжимаемой жидкости.

Раскрывая производные:

Уравнение Навье-Стокса совместно с уравнением неразрывности дают возможность решить основную задачу гидродинамики – определить поля скоростей давления и плотности в жидкости, движущейся под действием заданных сил.

Однако, уравнения Навье-Стокса не могут быть решены в общем виде (так как трудно определить граничные условия в неустановившемся потоке вязкой жидкости и др.), плотность и вязкость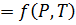

Решение получено только для некоторых простейших случаев движения жидкости.

Преобразование уравнений Навье-Стокса возможно методами теории подобия.

Для идеальной жидкости вязкость отсутствует и уравнение Навье-Стокса преобразуется в дифференциальные уравнения движения Эйлера.

Для неустановившегося движения:

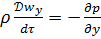
Раскрывая производные:

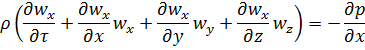
Это дифференциальные уравнения Эйлера для неустановившегося потока.

Для установившегося потока локальные изменения скорости равны нулю:

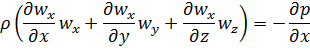
Это дифференциальные уравнения Эйлера для установившегося потока.

Дифференциальные уравнения являются основой для расчета процессов (интегрированием или при помощи теории подобия).