Формула Пуанкаре.

Предположим дополнительно, что кривая Γ (x = x(t), y = y(t), a ≤ t ≤ b) кусочно-гладкая, а векторное поле

Φ(x,y) = (φ(x,y),ψ(x,y))

непрерывно дифференцируемо в том смысле, что функции φ(x,y) и ψ(x,y) непрерывно дифференцируемы.

Пустьвектор

Φ(t) = (φ(x(t),y(t)),ψ(x(t),y(t)))

образуетсосьюабсциссуголα(t).Очевидно,

θ(t) = α(t) − α(a)

и

dθ = dα = darctg 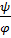= 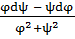. (1.14)

Отсюда вытекает, что

γ(Φ,Γ) = 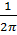(θ(b) − θ(a)) =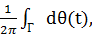

то есть

γ(Φ,Γ) = 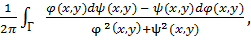(1.15)

Эта формула имеет смысл, так как знаменатель в подынтегральном выражении в нуль не обращается — вращение (как и угловая функция) определено лишь для непрерывных полей без нулевых векторов.

Если положить

φ(x(t),y(t)) = φ(t), ψ(x(t),y(t)) = ψ(t),

то формулу Пуанкаре (1.15) можно записать при помощи обыкновенного интеграла

γ(Φ,Γ) = 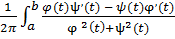dt.(1.16)

Для фактического вычисления вращения формула Пуанкаре малоудобна.