Поняття алгебраїчної операції
Ще в середній школі розглядають різноманітні числові множини: N, Z, Q, R, C. Якщо поставити завдання – проаналізувати, які спільні властивості мають ці множини і чим відрізняються, то прийдемо до висновку, що для цього числові множини слід розглядати не самі по собі, а відносно певних математичних дій або математичних операцій.
N  Z
Z 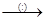 Q
Q 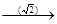 R
R 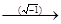 C.
C.
Отже, зазначені множини чисел відрізняються одна від одної здійсненністю або нездійсненністю в них тих чи інших математичних операцій.
У цьому ж проявляється і спільність властивостей цих числових множин. Справді, є операції, які здійсненні у кожній з них. Це дві основні дії арифметики – додавання і множення, відносно яких інші арифметичні дії виступають як залежні, а саме – як обернені. Яку б названих множин ми не взяли, дії додавання і множення можна виконувати над довільними двома елементами цієї множини.
Крім того, основні закони цих дій – комутативний, асоціативний, дистрибутивний – справедливі в кожній з цих множин.
З цього випливає, що однією з найважливіших характеристик числових множин є можливість виконувати над її елементами ті чи інші операції (насамперед, + і *), не виходячи за межі цієї множини.
Наведемо властивості дій додавання і множення.
Властивості додавання:
1) для довільних елементів а і b даної множини існує єдиний елемент с цієї ж множини такий, що 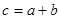 (с називають сумою, а а і b – доданками);
(с називають сумою, а а і b – доданками);
2) асоціативність додавання: 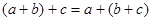 ;
;
3) для довільного елемента а даної множини існує єдиний нульовий елемент q такий, що 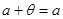 (роль q відіграє 0);
(роль q відіграє 0);
4) для довільного елемента а даної множини існує єдиний протилежний елемент -а такий, що 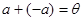 .
.
Властивості множення:
5) для довільних елементів а і b даної множини існує єдиний елемент с цієї ж множини такий, що 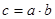 (с називають добутком, а а і b – множниками);
(с називають добутком, а а і b – множниками);
6) асоціативність множення: 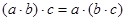 ;
;
7) для довільного елемента а даної множини існує єдиний одиничний елемент е такий, що 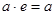 (роль е відіграє 1);
(роль е відіграє 1);
8) для довільного елемента а даної множини існує єдиний обернений елемент а-1 такий, що 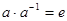 .
.
Властивості додавання і множення аналогічні, тому їх можна об’єднати, якщо назвати елементи q і е нейтральними, а –а і а-1 – симетричними. Очевидно, нейтральний елемент симетричний сам собі.
Означення 3.1.1. Нехай М – множина елементів довільної природи. Кажуть, що в М введено якусь алгебраїчну операцію, якщо довільним двом елементам з даної множини 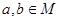 поставлено у відповідність єдиний третій елемент
поставлено у відповідність єдиний третій елемент 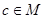 .
.
Довільну бінарну операцію позначають *:
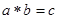 .
.
Отже, операція * є допустимою і однозначною.
Дата добавления: 2014-12-22; просмотров: 1067;
