Означення і приклади груп

Означення 3.1.2. Непорожню множину G елементів довільної природи, в якій введено якусь бінарну алгебраїчну операцію *, називають групою, якщо виконуються такі умови:

1) операція * – асоціативна: ;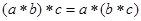

2) існує єдиний нейтральний елемент 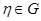такий, що для довільного 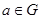: 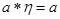і ;

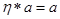3) існує єдиний симетричний елемент 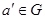такий, що для довільного 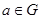: 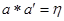і .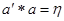

Властивості 1)-3) називають аксіомами групи.

Очевидно, визначена в групі G бінарна операція * не обов’язково комутативна. Якщо ж вона комутативна, то G називають комутативною або абелевою групою (Абель – норвезький математик, який вивчав рівняння, теорія яких тісно пов’язана з теорією комутативних груп).

Групу G називають скінченною, якщо множина її елементів – скінченна, і нескінченною у протилежному випадку. Кількість елементів скінченої групи називають її порядком.

Якщо в групі G бінарну операцію * називають додаванням і використовують відповідну символіку (+), то G називають адитивною групою. А якщо в групі G бінарну операцію * називають множенням і використовують відповідну символіку (×), то G називають мультиплікативною групою. Якщо в групі G бінарну операцію * називають додаванням і використовують відповідну символіку (+), то G називають адитивною групою.

Приклади груп.

1. Множина всіх цілих чисел Z є абелевою адитивною групою (у Z визначена операція додавання, яка асоціативна і комутативна. У множина Z існує єдиний нейтральний елемент 0. Кожне ціле число а має симетричне (-а)Î Z. Отже, всі аксіоми групи виконуються).

2. Множина всіх раціональних чисел Q і множина всіх дійсних чисел R є абелевими адитивними групами.

3. Множина всіх парних чисел є абелевою адитивною групою.

4. Множина всіх додатних раціональних чисел Q₊ – абелева адитивна група.

5. Множина всіх відмінних від 0 дійсних чисел R\{0}є абелевою мультиплікативною групою.

6. Множина всіх додатних дійсних чисел R₊і множина всіх відмінних від 0 дійсних чисел R\{0} – абелеві мультиплікативні групи.

7. Послідовність чисел 1 і –1 є абелевою мультиплікативною групою.

8. Множина, що складається з одного числа 0, є абелева адитивна група.

Очевидно, що множина непарних чисел не є групою відносно додавання, бо в ній не визначена операція +: додавання непарних чисел виходить за межі цієї множини (може бути парним числом).

Може статися, що частина Н елементів групи G є у свою чергу групою. Тоді Н називають підгрупою групи G.

Означення 3.1.3. Підмножину Н групи G називають підгрупою групи G, якщо Н є групою відносно бінарної операції *, визначеної в групі G.