Визначення хроматичного числа. Хроматичний поліном

Для обчислення хроматичного числа вводять функцію p(G,l).

Означення 2.5.6. Для заданого графа G і натурального числа l через p(G,l) (хроматичний поліном) позначається кількість всіх правильних розфарбувань графа G з допомогою l фарб.

Слід відмітити що наступна формула справедлива для достатньо малих S₀.

Теорема 2.5.2. Справедлива формула:

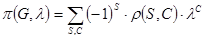, де

S – кількість ребер суграфів графа G;

С – кількість компонент зв’язаності суграфів графа G;

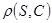- кількість суграфів графа G.

Якщо суграфів немає, то .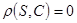

Ця формула дає змогу прослідкувати такі властивості функції p(G,l):

1) p(G,l) це многочлен степеня S₀ з коефіцієнтом 1 при старшому члені;

2) p(G,l) ділиться на l.

Нариклад, за теоремою 2.5.2 обчислимо p(G,l) для трикутного графа G.

Розпишемо кожен з випадків, нагадавши, що сам граф є своїм суграфом (випадок г):

а) S=0, C=3,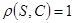

б) S=1, C=2,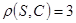

в) S=2, C=1,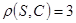

г) S=3, C=1, .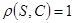

Тоді .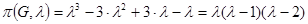

Простим перебором чисел від 1, знаходимо хроматичне число. Підставивши у цю формулу 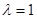або 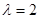, отримаємо, що p(G,1)=p(G,2)=0, тобто кількість правильних розфарбувань графа однією чи двома фарбами дорівнює нулеві – однією або двома фарбами граф розфарбовувати не можна. Хроматичне число цього графа є 3, оскільки його підставляння у формулу дало позитивний результат:

p(G,3)=1×2×3=3!=6

Властивості хроматичних поліномів:

1) p(G,l)= p(G₁,l)×p(G₂,l) (якщо G(p,l) складається з двох незв’язних частин, то розфарбування можна вибирати незалежно для двох незв’язних графів).

2) p(G,l)= 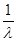p(G₁,l)×p(G₂,l) (якщо граф G отримано з двох графів склеюванням в одній точці х₀).

3) p(G,l)= 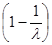p(G₁,l)×p(G₂,l) (якщо граф G отримано з двох незв’язних графів склеюванням по ребру, зовнішньому для обох графів).

4) p(G,l)= p(G₁,l)-p(G’,l) (якщо граф G отримано з G₁ доданням ребра без зміни вершин, G’ – граф, отриманий з G₁ склеюванням вершин, які інцидентні доданому ребру).

Граф G є однохроматичним тоді і тільки тоді, коли він не містить ні одного ребра; двохроматичним – тоді і тільки тоді, коли він не містить циклів непарної довжини.

Для розфарбування граней, утворених перетином прямих ліній на площині достатньо двох кольорів.

Необхідною і достатньою умовою розфарбування двома кольорами є те, що кожна вершина повинна мати парний степінь ³ 2.