Ранг та цикломатичне число графа

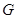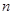Розглянемо граф на вершинах і 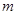ребрах, який має 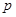компонент зв’язності.

Означення 2.3.2. Рангом графа 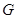називають число, яке дорівнює різниці між кількістю його вершин і компонент зв’язності:

.

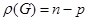Означення 2.3.3. Цикломатичним числом графа 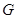називають число, яке дорівнює різниці між кількістю його ребер і вершин плюс кількість компонент компонент зв’язності:

.

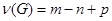Зауважимо, що існує зв’язок між рангом і цикломатичним числом графа:

.

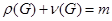Ранг і цикломатичне число – найважливіші характеристики графа.

Теорема 2.3.2. Нехай 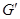граф, одержаний з графа 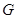додаванням нового ребра між вершинами 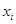та 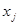. Тоді:

1) якщо 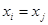чи вони можуть бути з’єднані ланцюгом в 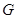, то

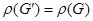та ;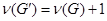

2) якщо 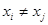чи вони не можуть бутиз’єднані ланцюгом в 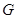, то

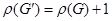та .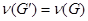

Доведення.

Якщо виконується умова 1), то додавання нового ребра кількості компонент зв’язності графа не змінює. Очевидно, що .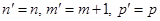

Тому

,

.

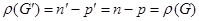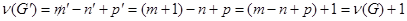Випадок 1) доведено.

Якщо ж виконується умова 2), то додане ребро – перешийок між компонентами зв’язності графа 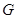, тому воно зменшує їх кількіть на 1.

У цьому випадку .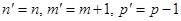

Тоді

,

.

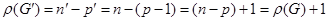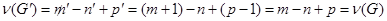Випадок 2) доведено. Теорему доведено¾.

Наслідок. .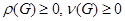

Доведення.