Поняття графа

Існують різні перетворення заданих графів, в результаті яких отримують нові графи. Ці перетворення називають операціями над графами.

2.2.1.1. Операція вилучення ребра (дуги). Якщо G(X,Г) – заданий граф і 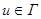– його ребро (дуга), то граф G₁(X,Г\{и}) називають графом, отриманим з G вилученням ребра (дуги). Кінцеві вершини вилученого ребра (дуги) із множини Х не вилучаються.

2.2.1.2. Операція вилучення вершини. Якщо G(X,Г) – заданий граф і 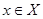– його вершина, то граф G₂(X\{х},Г) називають графом, отриманим з G вилученням вершини, якщо із множини Г вилучено всі ребра (дуги), інцидентні вилученій вершині.

2.2.1.3. Операція введення ребра (дуги). Якщо G(X,Г) – заданий граф, 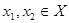– його вершини, причому 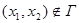, то граф G₃(X,ГÈ{(х₁,х₂)}) називають графом, отриманим з G введенням ребра (дуги).

2.2.1.4. Операція введення вершини. Якщо G(X,Г) – заданий граф, – його ребро (дуга) і , то граф G₄(XÈ{х},Г) називають графом, отриманим з G введенням вершини, якщо із множини Г вилучено ребро (дугу) 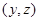і введено два нових – .

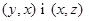2.2.1.5. Операція об’єднання графів. Якщо G(X,Г) і G*(X*,Г*) – задані графи, то граф G₅(XÈX*,ГÈГ*) називають об’єднанням графів G та G*.

2.2.1.6. Операція перерізу (перетину) графів. Якщо G(X,Г) і G*(X*,Г*) – задані графи, то граф G₆(XÇX*,ГÇГ*) називають перерізом графів G та G*.

2.2.1.7. Операція віднімання графів. Якщо G(X,Г) і G*(X*,Г*) – задані графи, то граф G₇(X,Г\Г*) називають різницею графів G та G*.

2.2.1.8. Операція строгої диз’юнкції графів. Якщо G(X,Г) і G*(X*,Г*) – задані графи, то реберно породжений граф G₈: [ГÅГ*] називають симетричною різницею графів G та G*.

2.2.1.9. Операція множення графів. Якщо G(X,Г) і G*(X*,Г*) – задані графи, то граф G₈(X´Х*,Г**) називають добутком графів G та G*, якщо тоді і тільки тоді, коли .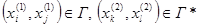

Для операції над матрицями при визначенні об’єднання, перетину, різниці, симетричної різниці використовують правила:

0È0=0 0Ç0=0 0\0=0 0Å0=0

0È1=1 0Ç1=0 0\1=0 0Å1=1

1È0=1 1Ç0=0 1\0=1 1Å0=1

1È1=1 1Ç1=1 1\1=1 1Å1=0

Щоб розглянути матрично добуток графів, впорядковують елементи Х´Х* так:

,

де п і т – кількості вершин графів G та G*, тобто .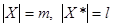

Тоді якщо А=||а_ij⁽¹⁾||, А*=||а_ij⁽²⁾|| – матриці суміжностей вершин графів G та G* відповідно, то А**=||b_(I,k),(j,l)||= а_ij⁽¹⁾×а_ij⁽²⁾ – матриця суміжності вершин графа G**=G´G*:

.

Наприклад, нехай задано графи G та G* так:

Здійснимо над цими графами всі описані вище операції.

Для геометричного зображення графа добутку, не беручи до уваги орієнтацію графів G та G*, побудуємо спочатку його матрицю суміжності вершин за матрицями суміжності вершин графів G та G*.

.

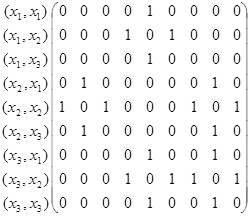Кожну вершину графа зображуємо впорядкованою парою і з’єднуємо відповідні пари за матрицею суміжності вершин.