Маршрути незамкнені (ланцюги, шляхи) і замкнені (цикли, контури). Повнота. Зв’язність. Сильна зв’язність
Коли задають або шукають певну послідовність ребер (дуг), то говорять про маршрути у графах..
Означення 2.1.13. Скінченну послідовність ребер (дуг) графа  (не обов’язково різних) називають маршрутом довжини п, якщо існує послідовність вершин
(не обов’язково різних) називають маршрутом довжини п, якщо існує послідовність вершин 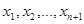 (не обов’язково різних), таких що
(не обов’язково різних), таких що  .
.
Вершини  і
і 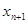 називають кінцевими або термінальними.
називають кінцевими або термінальними.
Означення 2.1.4. Маршрут називають відкритим або незамкненим, якщо  і замкненим у протилежному випадку.
і замкненим у протилежному випадку.
Означення 2.1.5. Незамкнений маршрут, у якого немає ребер (дуг), що повторюються, називають ланцюгом для неорієнтованого і шляхом для орієнтованого графа.
Означення 2.1.6. Замкнений маршрут, у якого немає ребер (дуг), що повторюються, називають циклом для неорієнтованого і контуром для орієнтованого графа.
Кажуть, що граф ациклічний або без контурний, якщо він не має циклів чи контурів.
Наприклад,

 – незамкнений маршрут;
– незамкнений маршрут;
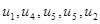 – замкнений маршрут;
– замкнений маршрут;
 – ланцюг;
– ланцюг;
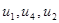 – цикл.
– цикл.
Граф називають повним, якщо будь-які його дві вершини суміжні.
Орієнтований граф G=(Х,Г) називають повним, якщо з того, що 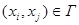 слідує, що
слідує, що  .
.
Означення 2.1.7. Неорієнтований граф G=(Х,Г) називають зв’язним, якщо в ньому існує ланцюг між кожною парою вершин.
Властивості зв’язних графів:
1) граф зв’язний тоді і тільки тоді, коли множину його вершин  не можна розбити на дві непорожні підмножини
не можна розбити на дві непорожні підмножини 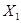 та
та  так, що дві граничні точки кожного ребра були в одній і тій самій множині;
так, що дві граничні точки кожного ребра були в одній і тій самій множині;
2) у зв’язному графі довільні два шляхи максимальної довжини мають спільну вершину;
3) якщо граф G=(Х,Г) – зв’язний, то граф G’=(Х,Г-u), отриманий в результаті видалення циклічного ребра и, також зв’язний.
Означення 2.1.8. Орієнтований граф називають зв’язним, якщо зв’язним є неорієнтований граф, що лежить в його основі.
Означення 2.1.9. Орієнтований граф G=(Х,Г) називають сильно зв’язним, якщо для кожної пари різних вершин  і
і 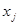 існує шлях з
існує шлях з  до
до 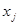 і навпаки – з
і навпаки – з 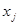 до
до  .
.
Дата добавления: 2014-12-22; просмотров: 1484;
