Ізоморфізм графів. Підграф. Суграф. Частковий граф
Нехай 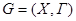 і
і 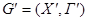 – графи і
– графи і 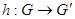 – взаємно однозначна відповідність.
– взаємно однозначна відповідність.
Означення 2.1.5. Відображення 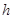 називають ізоморфізмом графів
називають ізоморфізмом графів 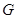 і
і 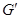 , якщо для довільних вершин
, якщо для довільних вершин  і
і 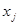 графа
графа 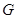 їх образи
їх образи 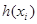 і
і 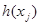 суміжні у графі
суміжні у графі 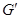 тоді і тільки тоді, коли
тоді і тільки тоді, коли  і
і 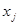 суміжні в
суміжні в 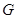 .
.
Якщо таке відображення існує, то графи 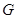 і
і 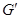 називають ізоморфними. Відношення ізоморфізму графів є відношенням еквівалентності.
називають ізоморфними. Відношення ізоморфізму графів є відношенням еквівалентності.
Означення 2.1.6. Підграфом G’(X’,Г’) графа G(X,Г) називають граф, у якого Х’ÌХ, Г’=ГÇ(Х´Х´N), тобто ребро (xi, xj) міститься в Г’ лише тоді, якщо xi та xj містяться в Х’, граф G називається надграфом графа G’.
Означення 2.1.7. Якщо всі вершини Х’=Х графа G присутні у підграфі G’, то G’ називають остовним підграфом G або суграфом.
Означення 2.1.8. Частковим графом G’(X’,Г’) графа G(X,Г) називають граф, у якого Х’ÌХ, Г’ÌГ.
Іншими словами, суграф отримуємо з графа видаленням деякої кількості дуг із збереженням всіх вершин, підграф – деякої кількості вершин разом з дугами цих вершин, а частковий граф – поєднання двох вищезгаданих операцій.
Наприклад:

Якщо множина вершин Х’ графа G’ є найменшою підмножиною Х, що містить всі кінцеві вершини ребер в Г’, то підграф G’ називають реберно породженим підграфом графа G і позначують 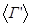 .
.
Якщо множина ребер Г’ графа G’ є найбільшою підмножиною Г такою, що кінцеві вершини всіх його ребер належать Х’, то G’ називають вершинно породженим підграфом графа G.
Означення 2.1.9. Граф 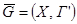 називають доповненням простого графа G=(Х,Г) якщо ребро (xi, xj) входить в Г’ лише тоді, коли воно не входить в Г.
називають доповненням простого графа G=(Х,Г) якщо ребро (xi, xj) входить в Г’ лише тоді, коли воно не входить в Г.
Дата добавления: 2014-12-22; просмотров: 1463;
