Відношення порядку
Означення 1.3.14. Бінарне відношення R називають відношенням строгого порядку, коли воно антисиметричне і транзитивне. Позначають: 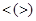 або
або 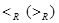 .
.
Отже R – відношення строгого порядку, якщо:
1) 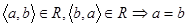 ;
;
2) 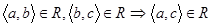 .
.
Наприклад, розташування символів у довільному скінченному алфавіті означує відношення строгого лексикографічного порядку, яке лежить в основі впорядкування словників, енциклопедій, індексів, довідників, списків, таблиць тощо.
Означення 1.3.15. Якщо відношення порядку є рефлексивним ( 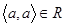 ), то його називають відношенням часткового (нестрогого) або квазіпорядку. Позначають:
), то його називають відношенням часткового (нестрогого) або квазіпорядку. Позначають: 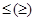 або
або 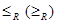 .
.
Наприклад, у числових множинах N, Q, R встановлено відношення строгого ( 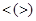 ) і нестрогого (
) і нестрогого ( 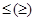 ) порядку.
) порядку.
Множину M, на якій задано відношення порядку, називають впорядкованою, аелементи a,bÎM – порівнюваними за відношенням R, якщо виконується 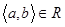 або
або 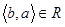 . Запис
. Запис  означає, що у множині
означає, що у множині 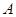 відношення порядку
відношення порядку 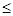 .
.
Впорядковану множину M, в якій будь-які різні два елементи є порівнюваними між собою, називають лінійно впорядкованою множиною або ланцюгом. Відповідне відношення R (як строге, так і нестроге), задане на лінійно впорядкованій множині, називають лінійним (досконалим) порядком.
Очевидно, відношення рівності є відношенням часткового порядку на будь-якій множині M, цей порядок називають тривіальним.
Теорема 1.3.3. Якщо 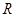 – відношення строгого (нестрогого) порядку, то обернене відношення
– відношення строгого (нестрогого) порядку, то обернене відношення  – теж відношення строгого (нестрогого) порядку.
– теж відношення строгого (нестрогого) порядку.
Нехай M частково впорядкована множина і A деяка непорожня підмножина множини M.
Означення 1.3.16. Верхньою гранню підмножини AÍM в множині M називається елемент bÎM такий, що a£b всіх aÎA. Елемент b називається найбільшим елементом множини M, якщо b – верхня грань множини M. Відповідно, елемент c частково впорядкованої множини M називається нижньою гранню підмножини AÍM, якщо c£a для будь-якого aÎA. Елемент c – найменший в множині M, якщо c – нижня грань самої множини M.
Означення 1.3.17. Елемент xÎM називається максимальним в множині M, якщо не існує елемента aÎM такого, що x<a. Відповідно, елемент nÎM називається мінімальним у множині M, якщо не існує елемента aÎM такого, що a<n.
У лінійно впорядкованій множині поняття найбільшого і максимального (найменшого і мінімального) елементів збігаються.
Дата добавления: 2014-12-22; просмотров: 1703;
