Бінарні відношення

Означення 1.2.3. Підмножина R декартового степеня Mⁿ деякої множини M називається n-місним або n-арним відношенням на множині M. Кажуть, що елементи a₁,a₂,...,a_nÎM знаходяться у відношенні R, якщо áa₁,a₂,...,a_nñÎR.

При відношення RÍM називають одномісним або унарним. Таке відношення часто називають також ознакою або характеристичною властивістю елементів множини M. Кажуть, що елемент aÎM має ознаку R, якщо aÎR і RÍM. Наприклад, ознаки “парність” і “кратність 3” виділяють із множини N натуральних чисел унарні відношення R¢ = {2k | kÎN } і R¢¢ = {3k | kÎN }, відповідно.

Найбільш популярними в математиці є двомісні або бінарні відношення ( ), на вивченні властивостей яких ми зупинимось детальніше. Далі скрізь під словом “відношення” розумітимемо бінарне відношення. Якщо елементи a,bÎM знаходяться у відношенні R (тобто áa,bñÎR), то це часто записують у вигляді aRb. Зауважимо, що бінарні відношення іноді розглядають, як окремий випадок відповідностей, а саме – відповідності між однаковими множинами.

Наприклад, на різних множинах можна задати такі бінарні відношення.

1. Відношення на множині N натуральних чисел:

R₁ - відношення “менше або дорівнює”, тоді 7R₁9, 2R₁2, 1R₁m для будь-якого mÎ N;

R₂ - відношення “ділиться на”, тоді 12R₂3, 49R₂7, mR₂1 для будь-якого mÎN ;

R₃ - відношення “складаються з однакових цифр”, тоді 107R₃701, 123R ₃3213311.

2. Відношення на множині точок координатної площини R²:

R₄ - відношення "знаходяться на однаковій відстані від початку координат", тоді (3,2) R₄ ( 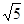,- ), (0,0)R ₄ (0,0) ;

R₅ - відношення “симетричні відносно осі ординат”, тоді (1,7)R₅(-1,7), а в загальному випадку (a,b)R₅(-a,b) для будь-яких a,bÎR ;

R₆ - відношення “менше або дорівнює”. Вважаємо, що (a,b)R₆(c,d), якщо a £ c і b £ d. Зокрема, (1,7)R₆(20,14), (-12,4)R₆(0,17).

3. Відношення на множині людей:

R₇ - відношення “є другом”,

R₈ - відношення “є молодшим за віком від”.

Слід звернути увагу на такі основні моменти:

- розглядуване відношення має місце не для всіх пар елементів заданих множин, а лише для деяких з них;

- не завжди якщо елемент x перебуває у відношенні з елементом y, то елемент y перебуває у тому самому відношенні з елементом x;

- кожне відношення між елементами даної множини можна розглядати як сукупність деяких впорядкованих пар декартового добутку двох однакових або різних множин.

Позначимо символом сукупність лівих координат впорядкованих пар бінарного відношення 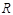, тобто:

.

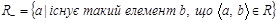Множину називають лівою областю або областю визначення відношення .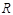

Аналогічно множину

називають правою областю або множиною значень відношення .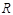

Наприклад, для відношення 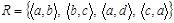, а .

Множину називають полем відношення 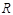. Для розглянутого прикладу .

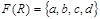Якщо будь-який елемент заданої множини перебуває у відношенні з будь-яким елементом цієї множини, то таке відношення називають універсальним. Якщо ж жоден елемент заданої множини не перебуває у відношенні з жодним елементом цієї множини, то таке відношення називають порожнім.

Відношення називають діагональним або одиничним.