Відношення еквівалентності
Означення 1.3.11. Бінарне відношення R називають відношенням еквівалентності, коли воно рефлексивне, симетричне і транзитивне.
Отже, R є відношенням еквівалентності, якщо:
1) 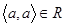 ;
;
2) 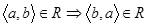 ;
;
3) 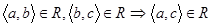 .
.
Якщо при цьому 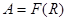 , то говорять, що
, то говорять, що 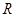 – відношення еквівалентності на множині
– відношення еквівалентності на множині 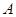 .
.
Наприклад, відношення 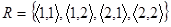 є відношенням еквівалентності.
є відношенням еквівалентності.
Відношеннями еквівалентності є також відношення рівності, рівно потужності множин, конгруентності, подібності, діагональне, порожнє та універсальне відношення.
Важливу роль відіграє в математиці відношення “мають однакову остачу при діленні на k” або “конгруентні за модулем k”, яке є відношенням еквівалентності на множині N натуральних чисел для будь-якого фіксованого kÎN. Відношення конгруентності за модулем k часто позначають a º b (mod k). Цьому відношенню належать, наприклад, пари натуральних чисел (17,22), (1221,6), (42,57) для k=5, тобто 17 º 22(mod 5), 1221 º 6 (mod 5), 42 º 57 (mod 5).
Нехай 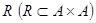 – відношення еквівалентності і
– відношення еквівалентності і 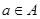 .
.
Означення 1.3.12. Переріз 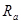 відношення
відношення 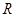 за елементом
за елементом 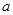 називають класом еквівалентності за відношенням
називають класом еквівалентності за відношенням 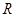 і позначають
і позначають 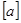 або
або 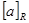 .
.
Отже, за означенням 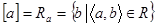 . Тобто клас еквівалентності
. Тобто клас еквівалентності 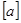 містить всі такі елементи множини
містить всі такі елементи множини 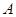 , які перебувають у відношенні
, які перебувають у відношенні 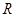 з елементом
з елементом 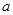 .
.
Наприклад, якщо 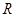 – відношення паралельності у площині
– відношення паралельності у площині 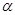 , а
, а 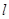 – деяка фіксована пряма у цій площині, то клас еквівалентності
– деяка фіксована пряма у цій площині, то клас еквівалентності 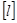 містить усі прямі площини
містить усі прямі площини 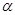 , паралельні прямій
, паралельні прямій 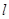 .
.
Теорема 1.3.1. Будь-які два класи еквівалентності за відношенням 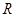 або не мають спільних елементів, або збігаються.
або не мають спільних елементів, або збігаються.
Теорема 1.3.2. Будь-яку множину 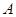 , в якій задано відношення еквівалентності
, в якій задано відношення еквівалентності 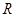 , можна подати у вигляді об’єднання різних класів еквівалентності за відношенням
, можна подати у вигляді об’єднання різних класів еквівалентності за відношенням 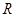 , тобто
, тобто 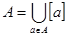 .
.
Означення 1.3.13. Множину всіх класів еквівалентності за відношенням 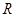 називають фактор-множиною множини
називають фактор-множиною множини 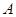 за відношенням
за відношенням 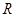 :
: 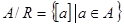 або
або 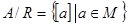 , де
, де 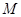 – сукупність таких елементів множини
– сукупність таких елементів множини 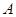 , яким відповідають різні класи еквівалентності.
, яким відповідають різні класи еквівалентності.
Наприклад, якщо 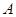 – сукупність всіх студентів певної групи, які отримали за іспит оцінку
– сукупність всіх студентів певної групи, які отримали за іспит оцінку 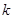 , а
, а 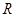 – відношення еквівалентності, що визначається умовою
– відношення еквівалентності, що визначається умовою 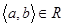 тоді і тільки тоді, коли
тоді і тільки тоді, коли 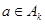 і
і 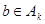 , то
, то 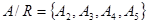 . Фактор-множина для відношення “конгруентні за модулем 3” на множині N натуральних чисел складається з трьох класів { 3k | kÎN }, { 3k-1 | kÎN } і { 3k-2 | kÎN}.
. Фактор-множина для відношення “конгруентні за модулем 3” на множині N натуральних чисел складається з трьох класів { 3k | kÎN }, { 3k-1 | kÎN } і { 3k-2 | kÎN}.
Потужність фактор-множини |А/R| називають індексом розбиття або індексом відношення еквівалентності R.
Нехай R відношення еквівалентності на множині А. Відображення множини А на фактор-множину А/R, яке кожному елементу aÎА ставить у відповідність клас еквівалентності 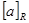 , називають канонічним або природним відображенням множини А на фактор-множину А/R.
, називають канонічним або природним відображенням множини А на фактор-множину А/R.
Дата добавления: 2014-12-22; просмотров: 1737;
