Рефлексивні, симетричні і транзитивні відношення
Означення 1.3.4. Бінарне відношення R називають рефлексивним у множині 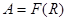 , якщо будь-який елемент
, якщо будь-який елемент 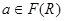 перебуває у відношенні сам з собою (
перебуває у відношенні сам з собою ( 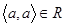 ).
).
Означення 1.3.5. Бінарне відношення R називають рефлексивним, якщо з того, що 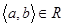 слідує, що
слідує, що 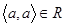 і
і 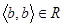 .
.
Наприклад, відношення 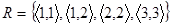 рефлексивне у множині
рефлексивне у множині 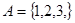 , проте не рефлексивне у множині
, проте не рефлексивне у множині  .
.
Рефлексивними є відношення рівності, подільності, паралельності, конгруентності, подібності фігур, універсальне та діагональне відношення.
Означення 1.3.6. Бінарне відношення R називають антирефлексивним (іррефлексивним) у множині 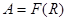 , якщо жоден елемент
, якщо жоден елемент 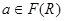 не перебуває у відношенні сам з собою (
не перебуває у відношенні сам з собою ( 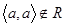 ).
).
Наприклад, відношення 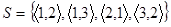 антирефлексивне у множині
антирефлексивне у множині 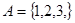 . Анти рефлексивними є відношення “не дорівнює”, “менше”, “більше”, перпендикулярності тощо.
. Анти рефлексивними є відношення “не дорівнює”, “менше”, “більше”, перпендикулярності тощо.
Порожнє відношення прийнято вважати як рефлексивним, так і антирефлексивним.
Якщо відношення є ні рефлексивним, ні анти рефлексивним, то його називають не рефлексивним.
Наприклад, відношення  не рефлексивне, оскільки елемент 2, на відміну від всіх інших, не перебуває у відношенні сам з собою
не рефлексивне, оскільки елемент 2, на відміну від всіх інших, не перебуває у відношенні сам з собою 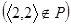 .
.
При зображенні рефлексивного відношення з допомогою графіка видно, що всі точки діагоналі  належать графіку відношення.
належать графіку відношення.
Означення 1.3.7. Бінарне відношення R називають симетричним, якщо з того, що 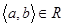 слідує, що
слідує, що 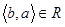 .
.
Наприклад, відношення 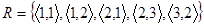 симетричне. Симетричними є відношення паралельності, перпендикулярності, подібності, конгруентності, універсальне відношення тощо.
симетричне. Симетричними є відношення паралельності, перпендикулярності, подібності, конгруентності, універсальне відношення тощо.
Для симетричного відношення його графік симетричний відносно діагоналі – бісектриси координатного кута.
Означення 1.3.8. Бінарне відношення R називають антисиметричним, якщо з того, що 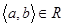 слідує, що
слідує, що  .
.
Наприклад, відношення 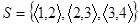 антисиметричне. Антисиметричними є відношення включення, “менше”, “більше”, “менше дорівнює” тощо.
антисиметричне. Антисиметричними є відношення включення, “менше”, “більше”, “менше дорівнює” тощо.
Відношення рівності, діагональне та порожнє вважають як симетричними, так і антисиметричними.
Означення 1.3.9. Бінарне відношення R називають транзитивним, якщо з того, що 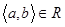 і
і 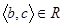 слідує, що
слідує, що 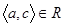 .
.
Наприклад, відношення 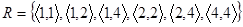 транзитивне. Транзитивними також є відношення “менше”, “більше дорівнює”, подільності, паралельності, подібності, включення, діагональне, порожнє та універсальне відношення тощо.
транзитивне. Транзитивними також є відношення “менше”, “більше дорівнює”, подільності, паралельності, подібності, включення, діагональне, порожнє та універсальне відношення тощо.
Не транзитивними є відношення “не дорівнює”, перпендикулярності, належності тощо.
Графік транзитивного відношення має властивість 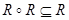 і навпаки.
і навпаки.
Операція обернення зберігає 5 властивостей відношень: рефлективність, антирефлексивність, симетричність, антисиметричність і транзитивність.
Означення 1.3.10. Відношення R* називають транзитивним замиканням відношення R на множині А, якщо 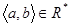 тоді і тільки тоді, коли у множині А існує послідовність елементів
тоді і тільки тоді, коли у множині А існує послідовність елементів 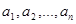 така, що
така, що 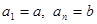 і
і 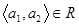 ,
, 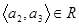 , ...,
, ..., 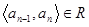 .
.
Наприклад, нехай 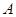 – множина точок на площині і
– множина точок на площині і 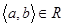 ,
,  , якщо точки
, якщо точки 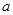 і
і 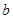 з’єднані відрізком. Тоді
з’єднані відрізком. Тоді 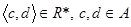 , якщо існує ламана лінія, яка з’єднує точки
, якщо існує ламана лінія, яка з’єднує точки  і
і 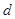 .
.
Дата добавления: 2014-12-22; просмотров: 3102;
