Відображення і функції
Означення 1.3.18. Відношення 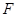 , задане на множинах
, задане на множинах 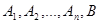 називають функціональним, якщо для будь-якого елемента
називають функціональним, якщо для будь-якого елемента 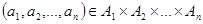 існує не більше одного елемента
існує не більше одного елемента 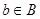 , такого, що
, такого, що 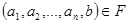 .
.
Якщо ж деякого 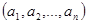 такий елемент
такий елемент 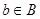 існує, то його позначають
існує, то його позначають 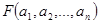 і записують
і записують 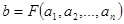 .
.
Нехай 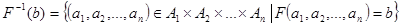 . Очевидно, для будь-якого функціонального відношення
. Очевидно, для будь-якого функціонального відношення 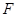 , заданого на множині
, заданого на множині 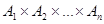 виконується включення
виконується включення 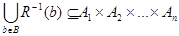 , де
, де 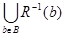 – область визначення відображення. Коли ж
– область визначення відображення. Коли ж 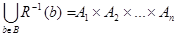 , то відношення
, то відношення 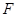 називають повністю визначеним, у випадку
називають повністю визначеним, у випадку 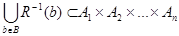 – частково визначеним або частковим.
– частково визначеним або частковим.
Означення 1.3.19. Відношення 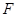 , задане на множинах
, задане на множинах 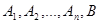 називають відображенням або функцією, якщо
називають відображенням або функцією, якщо 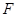 – функціональне і часткове. Позначують:
– функціональне і часткове. Позначують: 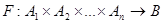 .
.
Число 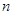 називають арністю функції
називають арністю функції 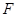 .
.
Якщо 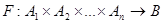 та існує
та існує 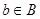 , такий, що
, такий, що 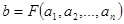 , то елемент
, то елемент 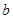 називають образом елемента
називають образом елемента 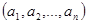 при відображенні
при відображенні 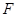 , а
, а 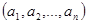 – прообразом елемента
– прообразом елемента 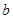 .
.
Відношення 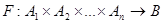 називають відображенням тоді і тільки тоді, коли для довільного
називають відображенням тоді і тільки тоді, коли для довільного 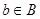 :
: 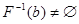 . Множину всіх таких елементів
. Множину всіх таких елементів 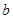 називають множиною значень відображення
називають множиною значень відображення 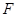 .
.
Відображення 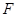 множини
множини 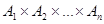 на множину
на множину 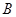 називають взаємно однозначним відображенням або взаємно однозначною відповідністю тоді і тільки тоді, коли обернене відношення
називають взаємно однозначним відображенням або взаємно однозначною відповідністю тоді і тільки тоді, коли обернене відношення 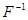 є відображенням В на
є відображенням В на 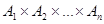 .
.
Дата добавления: 2014-12-22; просмотров: 930;
