Потужність множин

Усі введені вище теоретико-множинні операції та їхні властивості мають місце як для скінченних, так і для нескінченних множин. Суттєва різниця між скінченними та нескінченними множинами виявляється, коли мова заходить про “кількість елементів” та при спробі порівняти такі множини за “кількістю елементів”. Тут слова “кількість елементів” беруться в лапки тому, що зрозуміла умовність та невизначеність цього поняття для нескінченних множин.

Одними з основних досягнень канторівської теорії множин є поширення поняття “кількість елементів” зі скінченних множин на нескінченні та формулювання принципу, за яким можна порівнювати за “кількістю елементів” нескінченні множини. Зокрема, несподіваним та незвичайним виявився той факт, що різні нескінченні множини можуть мати різну “кількість елементів”, тобто для нескінченностей також існує своя ієрархія.

Канторівська ідея ґрунтується на такому спостереженні: для того щоб порівняти за кількістю елементів дві скінченні множини, зовсім необов’язково перелічувати елементи кожної з них. Можна діяти таким чином. Наприклад, необхідно порівняти за кількістю дві множини – множину S студентів та множину M всіх місць в аудиторіях. Запропонуємо кожному студенту зайняти одне місце. Якщо кожен студент отримає місце і при цьому в аудиторіях не залишиться жодного вільного місця, то очевидно, що кількість елементів в обох множинах S і M однакова. У протилежному випадку, множина S містить більше елементів ніж множина M, або навпаки. Очевидно, що запропонована процедура встановлює деяку функціональну відповідність між множинами S і M. У першому випадку ця відповідність виявляється взаємно однозначною, тоді коли у другому і третьому випадках умови взаємної однозначності не виконуються: або порушується умова повної визначеності (принаймні один студент не дістав місця), або порушується умова сюр’єктивності (хоча б одне місце залишилося вільним).

Кількість елементів множини A прийнято позначати через |A|.

Отже, неважко переконатися, що між двома скінченними множинами A і B існує взаємно однозначна відповідність тоді і тільки тоді, коли |A|=|B|.

Сформульоване твердження дозволяє розв’язувати задачу обчислення кількості елементів множини A шляхом встановлення взаємно однозначної відповідності між множиною A і деякою множиною B, кількість елементів якої відома або легко може бути визначена.

Означення 1.1.9. Елементи двох множин A і B перебувають у взаємно однозначній відповідності, якщо кожному елементу 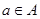відповідає єдиний елемент і, навпаки, кожен елемент є зіставленим єдиному елементу .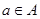

Множини A і B назвемо еквівалентними або рівнопотужними, якщо існує взаємно однозначна відповідність між множинами A і B.

Якщо еквівалентність множин A і B позначити через A~B, то безпосередньо з означення випливають такі властивості еквівалентності:

§ A~A (рефлексивність);

§ Якщо A~B, то B~A (симетричність);

§ Якщо A~B і B~C, то A~C (транзитивність).

Наведемо декілька прикладів еквівалентних нескінченних множин.

1) Множина натуральних чисел N еквівалентна множині квадратів натуральних чисел N²={1,4,9,16,...}. Взаємно однозначна відповідність встановлюється за законом: кожне натуральне число має єдиний квадрат, і навпаки, кожен елемент множини N ² має єдиний корінь у множині N , тобто (n,n²), nÎ N, п²Î N ².

2) Множина Z всіх цілих чисел еквівалентна множині P всіх парних чисел. Тут взаємно однозначна відповідність встановлюється так: (n,2n), nÎZ, 2nÎP.

3) Множина точок інтервалу (-p/2, p/2) еквівалентна множині точок дійсної прямої. Шукана взаємно однозначна відповідність встановлюється за допомогою тригонометричної функції tg: (x,tg x), xÎ(-p/2, p/2), tg xÎ(-¥,¥).

4) Множини точок двох довільних відрізків a і b еквівалентні. Правило, за яким встановлюється взаємно однозначна відповідність між точками відрізків a і b різної довжини, зображено на рисунку. Кожний промінь з точки O, який перетинає відрізки a і b в точках v і w, утворює одну пару (v,w) необхідної взаємно однозначної відповідності.

Множина A еквівалентна множині N натуральних чисел називається зліченною множиною.

Іншими словами, зліченна множина A – це така множина, всі елементи якої можна занумерувати числами 1,2,3,..., тобто можна вказати спосіб, за яким першому елементу множини A ставиться у відповідність число 1, другому – число 2, третьому – число 3 і т.д. Отже, будь-яку зліченну множину A можна подати у вигляді

A = {a₁, a₂, a₃, ..., a_n, ...}.

Неважко переконатись, що множини квадратів натуральних чисел, усіх парних чисел, усіх непарних чисел, чисел кратних деякому числу k, чисел, які закінчуються парою цифр 00 тощо є зліченними множинами.

Теорема Кантора. Множина всіх дійсних чисел з інтервалу (0,1) незліченна.

Будь-яка множину, еквівалентну множині всіх дійсних чисел з інтервалу (0,1), називають континуальною, або множиною потужності континуум.