Операції над множинами та їхні властивості
Для множин можна ввести ряд операцій (теоретико-множинних операцій), результатом виконання яких будуть також множини. За допомогою цих операцій можна конструювати із заданих множин нові множини.
Нехай A і B – деякі множини.
1.1.6.1. Означення 1.1.4. Об’єднанням множин A і B (позначають AÈB ) називають множину тих елементів, які належать хоча б одній з множин A чи B. Символічно операція об’єднання множин записується так
AÈB = {x | xÎA або xÎB} або xÎAÈB Û  .
.
Наприклад, {a,b,c}È{a,c,d,e}={a,b,c,d,e}.
Властивості об¢єднання множин:
1) комутативність: AÈB = BÈA;
2) асоціативність: (AÈB)ÈC = AÈ(BÈC);
3) ідемпотентність AÈA = A;
4) AÈÆ = A;
5) AÈЕ = Е.
1.1.6.2. Означення 1.1.5. Перетином (перерізом) множин A і B (позначають A Ç B ) називають множину, що складається з тих і тільки тих елементів, які належать множинам A і B одночасно. Тобто
AÇB = {x | xÎA і xÎB} або xÎAÇB Û  .
.
Наприклад, {a,b,c}Ç{a,c,d,e} = {a,c},
{a,b,c}Ç{d,e} = Æ.
Кажуть, що множини A і B не перетинаються, якщо AÇB = Æ.
Операції об’єднання та перетину множин можуть бути поширені на випадок довільної сукупності множин {Ai | iÎ N }. Так об’єднання множин Ai (записується  Ai ) складається з тих елементів, які належать хоча б одній з множин Ai даної сукупності. А перетин множин A (записується
Ai ) складається з тих елементів, які належать хоча б одній з множин Ai даної сукупності. А перетин множин A (записується  Ai) містить тільки ті елементи, які одночасно належать кожній з множин Ai.
Ai) містить тільки ті елементи, які одночасно належать кожній з множин Ai.
Властивості перерізу множин:
1) комутативність: AÇB = BÇA;
2) асоціативність: (AÇB)ÇC = AÇ(BÇC);
3) дистрибутивність операції Ç відносно операції È: AÇ(BÈC)=(AÇB)È(AÇC);
4) дистрибутивність операції È відносно операції Ç: AÈ(BÇC)=(AÈB)Ç(AÈC);
5) ідемподентність: AÇA = A;
6) AÇÆ = Æ;
7) AÇЕ = A;
8)  AÇ(AÈB) = A;
AÇ(AÈB) = A;
9) AÈ(AÇB) = A.
1.1.6.3. Означення 1.1.6. Різницею множин A і B (записується A\B ) називають множину тих елементів, які належать множині A і не належать множині B. Отже,
A \ B = { x | xÎA і xÏB} або xÎA \ B Û  .
.
Наприклад, {a,b,c} \ {a,d,c} = {b},
Z \ Z+=Z–,
{a,b} \ {a,b,c,d} = Æ.
Властивості різниці множин:
1) А \ А=Æ;
2) А \Æ=А;
3) А \ Е=Æ;
4) А \ В ¹ В \ А – різниця не комутативна;
5) (А \ В) \ С ¹ А \ (В \ С) – різниця не асоціативна;
6) (B È C) \ А = (В \ А) È (С \ А) – правий закон дистрибутивності операції \ відносно операції È;
7) (B Ç C) \ А = (В \ А) Ç (С \ А) – правий закон дистрибутивності операції \ відносно операції Ç.
1.1.6.4. Означення 1.1.7. Симетричною різницею множин A і B (записують ADB, AÅB або A¸B ) називають множину, що складається з усіх елементів множини A, які не містяться в B, а також усіх елементів множини B, які не містяться в A. Тобто
AÅB = { x | ( xÎA і xÏB ) або ( xÎB і xÏA )} або xÎAÅB Û  .
.
Наприклад, {a,b,c}Å{a,c,d,e} = {b,d,e},
{a,b}Å {a,b} = Æ.
Властивості симетричної різниці:
1) комутативність: AÅB = BÅA;
2) асоціативність: (AÅB)ÅC = AÅ(BÅC);
3) дистрибутивність операції Ç відносно операції Å: AÇ(BÅC)=(AÇB)Å(AÇC);
4) AÅA = Æ;
5) AÅÆ = А;
6) AÅB = (A \ В) È (В \ А).
Введені теоретико-множинні операції можна проілюструвати діаграмою (рис.1.1).

Рис. 1.1.
Тут множини A і B – це множини точок двох кругів.
Тоді AÈB – складається з точок областей І, ІІ, ІІІ,
AÇB – це область ІІ,
A \ B – область І,
B \ A – область ІІІ,
AÅB – області І і ІІІ.
1.1.6.5. Означення 1.1.8. Якщо зафіксована універсальна множина E, то доповненням множини A (яке є підмножиною універсальної множини E ) називають множину всіх елементів універсальної множини, які не належать множині A. Записують  .
.
Тобто
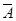 = { x | xÎE і xÏA } або xÎ
= { x | xÎE і xÏA } або xÎ 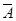 Û xÏA.
Û xÏA.
Неважко помітити, що 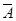 = E \ A.
= E \ A.
Наприклад, якщо за універсальну множину прийняти множину N всіх натуральних чисел, то доповненням  множини P всіх парних натуральних чисел буде множина всіх непарних натуральних чисел.
множини P всіх парних натуральних чисел буде множина всіх непарних натуральних чисел.
Властивості доповнення:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5) інволютивність:  ;
;
6)  ;
;
7) якщо А=В, то  ;
;
8) якщо 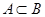 , то
, то  ;
;
9) правила (закони) де Моргана 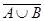 =
= 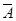 Ç
Ç  ;
;  =
= 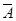 È
È  Зазначимо, що правила де Моргана припускають узагальнення для сукупності множин:
Зазначимо, що правила де Моргана припускають узагальнення для сукупності множин:
 ;
;  .
.
Приклад. Покажемо істинність однієї з наведених тотожностей – правила де Моргана.
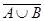 =
= 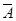 Ç
Ç  .
.
Доведемо спочатку, що 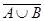 Í
Í 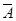 Ç
Ç  .
.
Нехай елемент xÎ 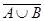 , тоді xÎE \ (A È B), тобто xÏA і xÏB, звідси xÎ
, тоді xÎE \ (A È B), тобто xÏA і xÏB, звідси xÎ 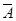 і xÎ
і xÎ  , отже, xÎ
, отже, xÎ 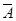 Ç
Ç  . Отже, за означенням підмножин:
. Отже, за означенням підмножин: 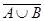 Í
Í 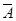 Ç
Ç  .
.
Дата добавления: 2014-12-22; просмотров: 3221;
