Рівність множин

Іноді означення рівності множин називають інтуїтивним принципом об’ємності (аксіомою екстенсіональності).

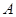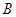Означення 1.1.2. Множини і називають рівними, якщо вони складаються з одних і тих самих елементів, тобто кожний елемент множини 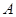є елементом множини 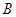і навпаки.

Записують: .

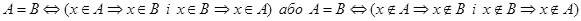
Наприклад, Z₊=N, N₊=N, [-2; 5]_- = [-2; 0).

Властивості рівності множин:

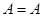§ – рефлексивність;

§ якщо , то 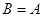– симетричність;

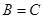§ якщо і , то 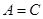– транзитивність.

Запис 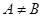означає, що принаймні одна з розглядуваних множин містить елемент, який не належить іншій.

Наприклад, Z₊¹Z, [-2; 5]₊ ¹ [-2; 5), {{a,b}}¹{a,b}, {(a,b)}¹{a,b}.