Елементи множини

Означення 1.1.1. Об’єкти, які утворюють дану множину, називають її елементами.

Елементами множини можуть бути найрізноманітніші об’єкти: парні числа, літери, люди, автомобілі на стоянці, картини в музеї тощо.

Множини, як правило, позначують великими латинськими літерами: A, B, C, …, M, …, а елементи множин – малими: a, b, c, …, m, … . Записують:

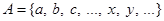(перелічивши всі елементи у фігурних дужках, якщо множина складається з невеликої кількості елементів), або

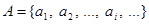(використовуючи змінні з індексами).

При цьому слід розрізняти загальний елемент множини , довільний – чи конкретний – .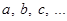

Для деяких найважливіших множин у математиці вживаються загальноприйняті позначення:

§ N – множина натуральних чисел;

§ Z – множина цілих чисел;

§ Q – множина раціональних чисел;

§ R – множина дійсних чисел;

§ С – множина комплексних чисел;

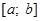§ – числовий проміжок (відрізок);

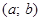§ – числовий інтервал тощо.

Якщо 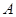– деяка числова множина, то через 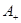позначують множину її додатних елементів, а через 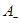– від’ємних.

Те, що об’єкт a є елементом множини M записуються так: aÎM (читають: “a належить множині M”, “a є елементом множини M”, “Множина М містить елемент а”, “а входить до множини М”). Знак належності елемента множині Î є стилізацією першої літери грецького слова esti (бути). Для того, щоб підкреслити, що деякий елемент a не належить множині M, вживають позначення aÏM, a 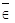M або .

Запис a,b,c,...ÎM використовують для скорочення запису aÎM, bÎM, cÎM,....

Множину називають скінченною, якщо кількість її елементів скінчена, тобто існує натуральне число k, що є кількістю елементів цієї множини. У протилежному разі множина є нескінченною.

Елементами множини можуть бути ще й інші множини. Наприклад, нехай множина 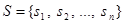– множина студентів деякої групи, які складали іспит. Цю множину можна означити й по-іншому: , де 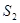– множина студентів, які склали іспит на оцінку “2”, відповідно , , 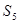– на “3”, “4” і “5”. У цьому випадку множини 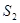, , , 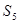називають підмножинами множини .

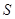Необхідно розрізняти такі два різні об’єкти, як елемент a і множина {a}, яка складається з єдиного елемента a.

Множину вважають заданою, якщо про кожен її об’єкт можна сказати є він елементом даної множини чи ні. Це дає змогу сформулювати інтуїтивний принцип абстракції (аксіома згортання): елементами множини є лише ті і тільки ті об’єкти, які мають певну характеристичну властивість.

Іноді може не існувати об’єктів, які мають характеристичну властивість для складання множини. Тоді кажуть, що ця властивість визначає порожню множину. Її позначують символом “ 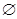”. Записують: , .

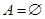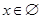Елементи множин можуть бути різними і рівними. Рівні (однакові) елементи мають такі властивості:

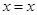§ – рефлексивність;

§ якщо , то 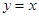– симетричність;

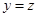§ якщо і , то – транзитивність.