Доведемо обернене включення: Ç Í .
Припустимо xÎ 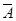 Ç
Ç  , це означає, що xÎ
, це означає, що xÎ 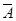 і xÎ
і xÎ  , тобто xÏA і xÏB, тому xÏAÈB, отже xÎ
, тобто xÏA і xÏB, тому xÏAÈB, отже xÎ 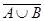 . Зі справедливості обох включень
. Зі справедливості обох включень 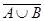 Í
Í 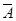 Ç
Ç  і
і 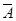 Ç
Ç  Í
Í 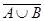 за законом антисиметричності для підмножин випливає істинність рівності
за законом антисиметричності для підмножин випливає істинність рівності 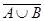 =
= 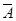 Ç
Ç  .
.
Твердження доведено. <
Аналогічно можуть бути доведені всі інші наведені теоретико-множинні тотожності. Ці тотожності дають змогу спрощувати різні складні вирази над множинами.
Приклад. (AÇBÇCÇ  )È(
)È( 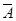 ÇC)È(
ÇC)È(  ÇC)È(CÇD) = (AÇBÇCÇ
ÇC)È(CÇD) = (AÇBÇCÇ  )È((
)È(( 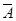 È
È  È D)ÇC) = = ((AÇBÇ
È D)ÇC) = = ((AÇBÇ  ) È (
) È ( 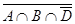 ))ÇC = EÇC = C. <
))ÇC = EÇC = C. <
Дата добавления: 2014-12-22; просмотров: 814;
