Якщо , то говорять про впорядковану пару, при .

Впорядковану пару елементів позначують або .

За допомогою поняття множини впорядковану пару означують так:

.

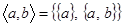Може статися, що впорядкована пара має однакові елементи:

.

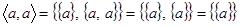Теорема 1.2.1. Рівність 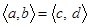справджується тоді і тільки тоді, коли 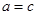і .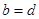

Оскільки елементи a і b впорядкованої пари – нерівноправні, то елемент 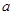називають першою (лівою) координатою (проекцією, компонентою), а – другою (правою) координатою (проекцією, компонентою) цієї пари.

Використовуючи поняття впорядкованої пари можна означити впорядковану трійку:

.

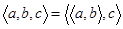У літературі впорядковані п-ки, зокрема пари, трійки, іноді називають п-вимірними (відповідно, двовимірними, тривимірними) векторами або кортежами.