Примеры. 1) Функция является первообразной для функции на всей числовой оси, так как при любом х: .

1) Функция 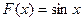является первообразной для функции 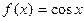на всей числовой оси, так как при любом х: .

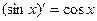2) Функция 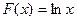является первообразной для функции 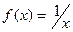на промежутке 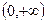, так как в каждой точке этого интервала выполнено равенство .

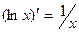Заметим, что задача отыскания по заданной функции 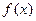ее первообразной не однозначна: если 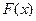первообразная, то и функция 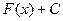, где С – произвольное постоянное число, также первообразная для функции 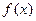, так как .

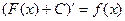Определение 1.7.2. Совокупность всех первообразных функций для 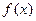на промежутке Х называется неопределенным интегралом от функции 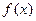на этом промежутке и обозначается символом

.

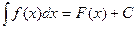В этом обозначении знак 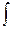называется знаком интеграла; 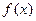- подынтегральной функцией; 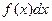- подынтегральным выражением, а переменная х – переменной интегрирования.

Операция нахождения первообразной по ее производной или неопределенного интеграла по данной функции называется интегрированием этой функции.