Метод замены переменной.

Пусть функция х = j (t) монотонна и имеет непрерывную производную на некотором промежутке изменения переменной t, функция f(x) непрерывна на интервале, принадлежащем области значений функции х = j (t), так что определена сложная функция f(j(t)). Тогда справедливо равенство

.

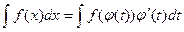Часто используются следующие варианты замены переменной:

1.

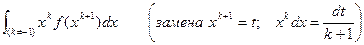
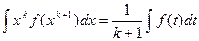
2.

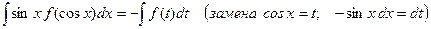
3.

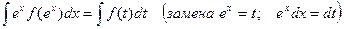
4.

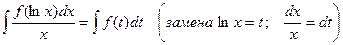
5.

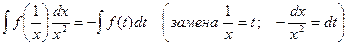
6.

Пример 2.Вычислить интегралы:

1.

Решение: Имеем . Положим , тогда 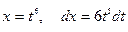. Находим 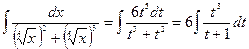. Выделяя делением целую часть дроби, получаем

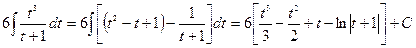
Окончательно

2. .

Решение: Преобразуем выражение .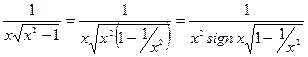

В результате получим . Сделаем замену переменной 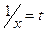, тогда - , откуда .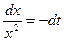

В итоге имеем: