Площадь плоской фигуры. Рассмотрим на плоскости 0xy фигуру, ограниченную графиком непрерывной и неотрицательной функции на отрезке
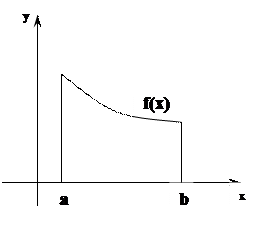
рис.1
Рассмотрим на плоскости 0xy фигуру, ограниченную графиком непрерывной и неотрицательной функции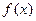 
на отрезке 
, отрезком и вертикальными прямыми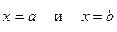 
(рис.1). Эта фигура называется криволинейной трапецией.
Площадь криволинейной трапеции равна определенному интегралу от функции 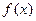на отрезке :
.
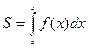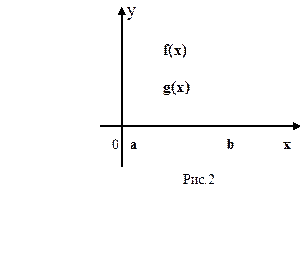
Если фигура ограничена сверху и снизу функциям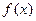и и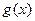 
соответственно, непрерывными на отрезке , причем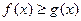 
, то площадь S криволинейной фигуры равна разности площадей криволинейных трапеций, ограниченных сверху графикам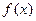и и :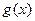
.
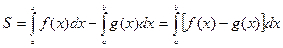Пример 3.Найти площадь фигуры, ограниченной линиями 
.
Решение: Вычислим абсциссы точек пересечения указанных кривых, для чего приравняем правые части этих уравнений: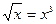 
. Корни уравнения 
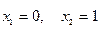. Следовательно, площадь фигуры дается определенным интегралом на отрезке 
:
.
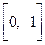1.9. КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО РАЗДЕЛУ «МАТЕМАТИЧЕСКИЙ АНАЛИЗ».
1. Задания по теме «Предел числовой последовательности»:
| Таблица А | |||
| № варианта | 1. По определению предела последовательности
доказать, что  :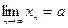
| 2. Вычислить следующие пределы: | |
| Вариант 1 |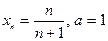 
| 
| 
|
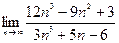
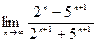
| Вариант 2 |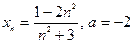 
| 
| 
|
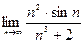
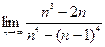
| Вариант 3 |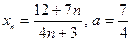 
| 
| 
|
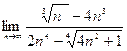
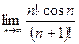
| Вариант 4 |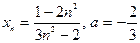 
| 
| 
|
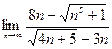
| Вариант 5 | 
| 
| 
|
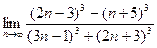
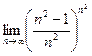
| Вариант 6 |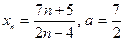 
| 
| 
|
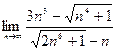
| Вариант 7 |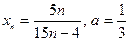 
| 
| 
|
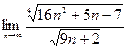
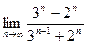
| Вариант 8 |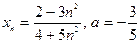 
| 
| 
|
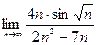
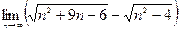
| Вариант 9 |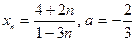 
| 
| 
|
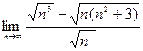
| Вариант 10 | 
| 
| 
|
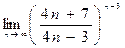
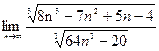
| Таблица Б | |||
| Вариант 11 |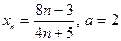 
| 
| 
|
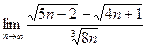
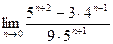
| Вариант 12 | 
| 
| 
|
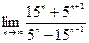
| Вариант 13 |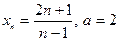 
| 
| 
|
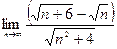
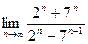
| Вариант 14 |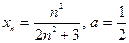 
| 
| 
|
| Вариант 15 |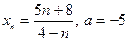 
| 
| 
|
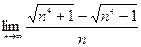
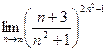
| Вариант 16 |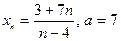 
| 
| 
|
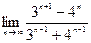
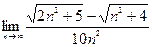
| Вариант 17 |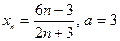 
| 
| 
|
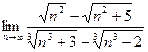
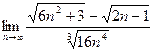
| Вариант 18 |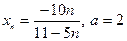 
| 
| 
|
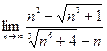
| Вариант 19 |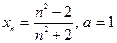 
| 
| 
|
| Вариант 20 | 
| 
| 
|
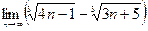
2. Задания по теме «Предел функции»:
| Таблица А | |||
| № варианта | Вычислить предел следующих функций: | ||
| Вариант 1 |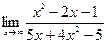 
| 
| 
|
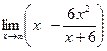
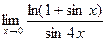
| Вариант 2 |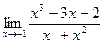 
| 
| 
|
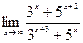
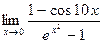
| Вариант 3 |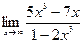 
| 
| 
|
| Вариант 4 |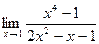 
| 
| 
|
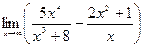
| Вариант 5 |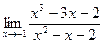 
| 
| 
|
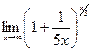
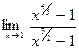
| Вариант 6 |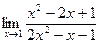 
| 
| 
|
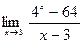
| Вариант 7 |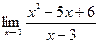 
| 
| 
|
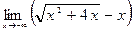
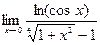
| Вариант 8 | 
| 
| 
|
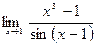
| Вариант 9 |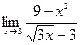 
| 
| 
|
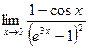
| Вариант 10 |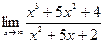 
| 
| 
|
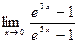
| Таблица Б | |||
| Вариант 11 |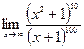 
| 
| 
|
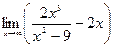
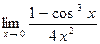
| Вариант 12 |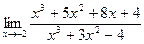 
| 
| 
|
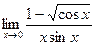
| Вариант 13 | 
| 
| 
|
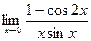
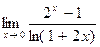
| Вариант 14 | 
| 
| 
|
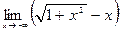
| Вариант 15 | 
| 
| 
|
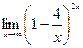
| Вариант 16 |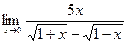 
| 
| 
|
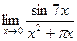
| Вариант 17 |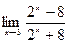 
| 
| 
|
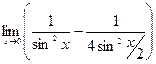
| Вариант 18 |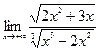 
| 
| 
|
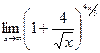
| Вариант 19 |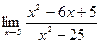 
| 
| 
|
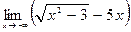
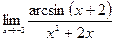
| Вариант 20 |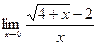 
| 
| 
|
3. Задания по теме «Дифференциальное исчисление»:
| Таблица А | ||
| № варианта | Вычислить производную функции: | Исследовать функцию и построить график: |
| Вариант |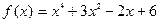 
| 
|
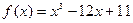
| Вариант | 
| 
|
| Вариант | 
| 
|
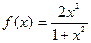
| Вариант | 
| 
|
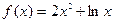
| Вариант | 
| 
|
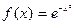
| Вариант |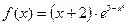 
| 
|
| Вариант |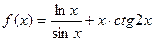 
| 
|
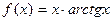
| Вариант |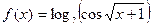 
| 
|
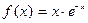
| Вариант |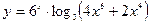 
| 
|
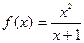
| Вариант | 
| 
|
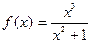
| Таблица Б | ||
| Вариант |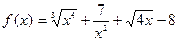 
| 
|
| Вариант |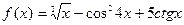 
| 
|
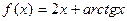
| Вариант | 
| 
|
| Вариант |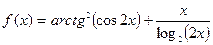 
| 
|
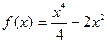
| Вариант | 
| 
|
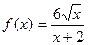
| Вариант | 
| 
|
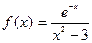
| Вариант |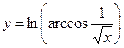 
| 
|
| Вариант | 
| 
|
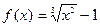
| Вариант |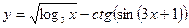 
| 
|
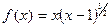
| Вариант |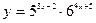 
| 
|
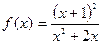
4. Задания по теме «Интегральное исчисление»:
| Таблица А | |||
| № варианта | Вычислить неопределенный интеграл: | Вычислить определенный интеграл: | Найти площадь фигуры, ограниченной заданными линиями: |
| Вариант 1 |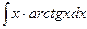 
| 
| 
|
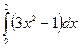
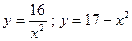
| Вариант 2 | 
| 
| 
|
| Вариант 3 | 
| 
| 
|
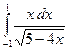
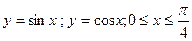
| Вариант 4 |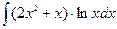 
| 
| 
|
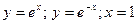
| Вариант 5 |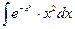 
| 
| 
|
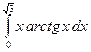
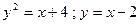
| Вариант 6 |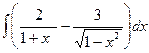 
| 
| 
|
| Вариант 7 | 
| 
| 
|
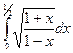
| Вариант 8 |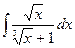 
| 
| 
|
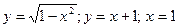
| Вариант 9 |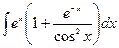 
| 
| 
|
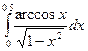
| Вариант 10 |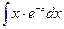 
| 
| 
|
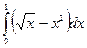
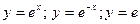
| Таблица Б | |||
| Вариант 11 |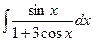 
| 
| 
|
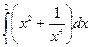
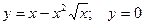
| Вариант 12 |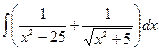 
| 
| 
|
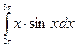
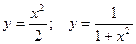
| Вариант 13 |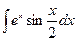 
| 
| 
|
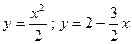
| Вариант 14 |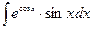 
| 
| 
|
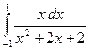
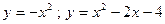
| Вариант 15 |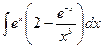 
| 
| 
|
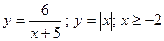
| Вариант 16 |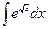 
| 
| 
|
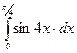
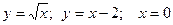
| Вариант 17 |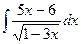 
| 
| 
|
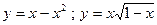
| Вариант 18 |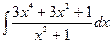 
| 
| 
|
| Вариант 19 |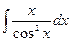 
| 
| 
|
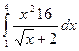
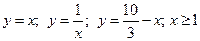
| Вариант 20 | 
| 
| 
|
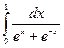
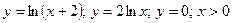
Дата добавления: 2014-12-04; просмотров: 1077;