Координаты центра тяжести плоской фигуры. Центр тяжести треугольника, сектора круга
Путем аналогичных рассуждений легко найти, что если тело представляет собой однородную плоскую и тонкую пластину, то для нее
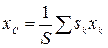 ,
, 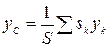 , (2)
, (2)
где 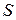 - площадь всей пластины;
- площадь всей пластины; 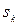 -площади ее частей. Точку, координаты которой определяются формулами (2), называют центром тяжести площади
-площади ее частей. Точку, координаты которой определяются формулами (2), называют центром тяжести площади  .
.
 1. Центр тяжести площади треугольника.
1. Центр тяжести площади треугольника.
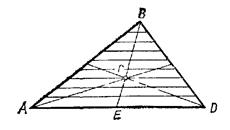
Разобьем площадь треугольника ABD прямыми, параллельными стороне AD, на n узких полосок; центры тяжести этих полосок будут лежать на медиане BE треугольника. Следовательно, и центр тяжести всего треугольника лежит на этой медиане. Аналогичный результат получается для двух других медиан. Отсюда заключаем, что центр тяжести площади треугольника лежит в точке пересечения его медиан.
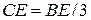 .
.
Для прямоугольного треугольника центр тяжести лежит на пересечении отрезков, откладываемых от прямого угла на расстояние 1/3 длины соответствующего катета.
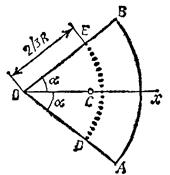 2. Центр тяжести площади кругового сектора. Рассмотрим круговой сектор ОАВ радиуса R с центральным углом
2. Центр тяжести площади кругового сектора. Рассмотрим круговой сектор ОАВ радиуса R с центральным углом 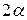 . Разобьем мысленно площадь сектора ОАВ радиусами, проведенными из центра О, на n секторов. В пределе, при неограниченном увеличении числа n, эти секторы можно рассматривать как плоские треугольники, центры тяжести которых лежат на дуге DE радиуса
. Разобьем мысленно площадь сектора ОАВ радиусами, проведенными из центра О, на n секторов. В пределе, при неограниченном увеличении числа n, эти секторы можно рассматривать как плоские треугольники, центры тяжести которых лежат на дуге DE радиуса 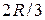 . Следовательно, центр тяжести сектора ОАВ совпадает с центром тяжести дуги DE, т.е. центр тяжести площади кругового сектора лежит на его оси симметрии на расстоянии от центра О, равном
. Следовательно, центр тяжести сектора ОАВ совпадает с центром тяжести дуги DE, т.е. центр тяжести площади кругового сектора лежит на его оси симметрии на расстоянии от центра О, равном
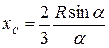 .
.
Дата добавления: 2014-12-22; просмотров: 5894;
