Условия равновесия системы сил. Теорема Вариньона о моменте равнодействующей относительно центра и оси
Условия равновесия: для равновесия любой системы сил необходимо и достаточно, чтобы главный вектор этой системы сил и ее главный момент относительно любого центра были равны нулю, т. е. чтобы выполнялись условия  ,
,  .
.
Эти условия являются необходимыми, так как если какое-нибудь из них не выполняется, то система действующих на тело сил приводится или к равнодействующей (когда  ), или к паре сил (когда
), или к паре сил (когда  ) и, следовательно, не является уравновешенной. Одновременно эти же условия являются и достаточными, потому что при
) и, следовательно, не является уравновешенной. Одновременно эти же условия являются и достаточными, потому что при  система сил может приводиться только к паре с моментом
система сил может приводиться только к паре с моментом  , а так как
, а так как  , то имеет место равновесие.
, то имеет место равновесие.
Теорема Вариньона о моменте равнодействующей: если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра О (оси z) равен сумме моментов сил системы относительно того же центра (оси z).
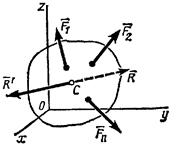 Пусть система сил
Пусть система сил  ,
,  , …
, …  приводится к равнодействующей
приводится к равнодействующей 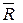 , линия действия которой проходит через некоторую точку С. Приложим в этой точке силу
, линия действия которой проходит через некоторую точку С. Приложим в этой точке силу  . Тогда система сил
. Тогда система сил  ,
, 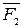 , …
, … 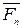 ,
,  будет находиться в равновесии и для нее должно выполняться условие
будет находиться в равновесии и для нее должно выполняться условие  , т. е. для данных сил (включая силу
, т. е. для данных сил (включая силу  ) должно быть
) должно быть  . Но так как
. Но так как  и обе силы направлены вдоль одной и той же прямой, то
и обе силы направлены вдоль одной и той же прямой, то 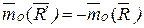 . Подставляя это значение
. Подставляя это значение 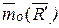 в предыдущее равенство, найдем из него, что
в предыдущее равенство, найдем из него, что
 .
.
Проецируя полученное равенство на ось z, проходящую через центр О, получим
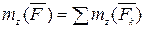
Тем самым теорема доказана. Ею часто бывает удобно пользоваться при вычислении моментов сил.
Дата добавления: 2014-12-22; просмотров: 2434;
