Координаты центра тяжести линии. Центр тяжести дуги окружности

Формулы для координат центра тяжести линии имеют вид:

, , ,

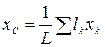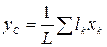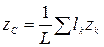где 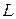- длина всей линии; 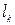- длины ее частей.

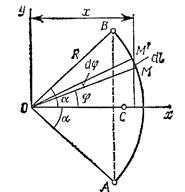
Центр тяжести дуги окружности. Рассмотрим дугу 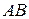радиуса 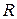с центральным углом 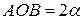. В силу симметрии центр тяжести этой дуги лежит на оси Ох. Найдем координату 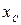. Для этого выделим на дуге АВ элемент ММ' длиной 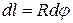, положение которого определяется углом 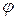. Координата х элемента ММ' будет 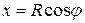. Подставляя эти значения х и 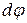в первую из формул:

,

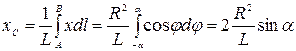где L — длина дуги АВ, равная 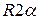. Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном

,

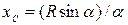где угол 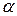измеряется в радианах.

26. Методы нахождения центра тяжести твёрдых тел. Статический момент площади плоской фигуры относительно оси.

1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии.

2. Разбиение. Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всего тела можно непосредственно вычислить по формулам:

, ,

.

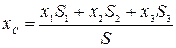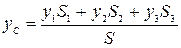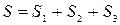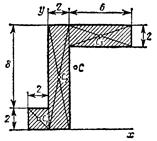
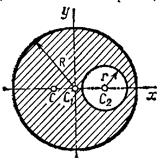3. Дополнение. Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известные.

, .

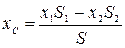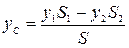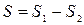
Существуют также различные экспериментальные методы определения центра тяжести тел.

Статический моментом площади плоской фигуры относительно оси называется сумма произведений элементарных площадей, входящих в состав плоской фигуры, на алгебраические значения их расстояний до данной оси.

В формулах координат центра тяжести плоской фигуры

,

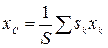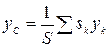
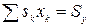- статический момент относительно оси Oy.

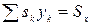- статический момент относительно оси Ox.

Из этих же формул , .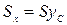

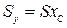Измеряется статический момент площади плоской фигуры относительно оси в см³.